SVM详细推导及拉格朗日对偶性思考

最近在阅读机器学习西瓜书SVM(Support Vector Mechine)部分的时候，其目标函数使用了拉格朗日乘子法并将其转化为拉格朗日对偶性问题进行求解，并且在后面引入软间隔的SVM也使用了同样的方法，因此自己在网上查阅了相关的资料对其原理进行探索，最后整理在下文。

SVM

原始问题

SVM尝试在给定样本集$D={(x_1, y_1),(x_2, y_2),…,(x_m, y_m)}, y_i\in${-1,+1}中找到一个划分超平面，将不同类别的样本分开，如下图：

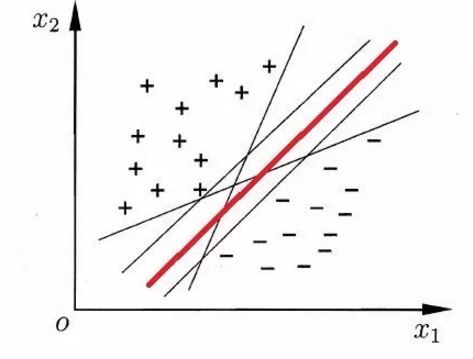
​ 根据结构风险最小化的原则，显然上图的红色的线是最好的划分超平面，因为该超平面所产生的分类是最鲁棒的，对未知样本的泛化能力最强。

​ 在样本空间中，划分超平面可通过如下线性方程来描述：

$$\omega^Tx+b=0 \tag{1}$$

在二维的情况下，超平面就是一条直线，令$w=[a,b]. x=[x,y], b=c$，因此线性方程为 $ax+by+c=0$

“其中$w=(w_1;w_2,;…;w_d)$为法向量，决定了超平面的方向；b为位移项，决定了超平面与原点之间的距离。显然，划分超平面可被法向量 $w$和 位移 $b$ 确定，下面我们将其记为$(w,b)$，样本空间中任意点 $x$ 到超平面 $(w,b)$ 的距离可写为:

$$r=\frac{\mid w^Tx+b \mid}{\parallel w \parallel}\tag{2}$$

在二维的情况下，$\parallel w \parallel =\sqrt{a^2+b^2} $。

假设超平面$(w,b)$能将训练样本正确分类，即对任意$(x_i,y_i) \in D$，若$y_i=+1$则有$w^Tx_i+b>0$；若$y_i=-1$，则有$w^Tx_i+b<0$。令：

$$\begin{cases} w^Tx_i+b\ge+1,&y_i=+1 \\ w^Tx_i+b\le-1,&y_i=-1 \end{cases} \tag{3}$$

换句话说，在分类正确的情况下，分类为 $+1$ 的样本$(x_i,y_i)$应该满足$w^Tx_i+b\ge+1$，分类为 $-1$ 的样本$(x_i,y_i)$应该满足$w^Tx_i+b\le-1$。如下图中距离超平面最近的几个训练样本 $\oplus$ 和 $\ominus$ 能使上式成立，它们被称为“支持向量”(support vector)，两个异类支持向量到超平面的距离之和为：

$$\gamma=\frac{2}{\parallel \omega \parallel} \tag{4}$$

它们被称为间隔(margin)。

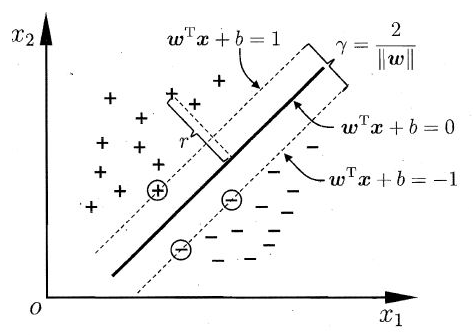
为了找到具有“最大间隔”(maximum margin)的划分超平面，也就是要找到能满足式(3)中约束的参数 $\omega$ 和 $b$ ，使得 $\gamma$ 最大，即：

$$\begin{align*} &\max_{\omega,b} \frac{2}{\parallel \omega \parallel} \\ &s.t \ \ \ \ y_i(\omega^Tx_i+b) \ge1, \ i=1,2,...,m \end{align*} \tag{5}$$

等价于：

$$\begin{align*} &\min_{\omega,b}\frac{1}{2} \parallel \omega \parallel^2 \\ &s.t \ \ \ \ y_i(\omega^Tx_i+b) \ge1, \ i=1,2,...,m \end{align*} \tag{6}$$

这就是支持向量机(Support Vector Machine，SVM)的基本型。

对于线性不可分的训练数据集，可以对每个样本点 $(x_i, y_i)$ 引进一个松弛变量 $\xi_i$，使得原问题的目标函数变为：

$$\begin{align*} \min_{\omega,b,\xi}\;&\frac{1}{2}||\omega||^2+C\sum_{i=1}^n\xi_i\\ s.t.\;\;&y_i(\omega x_i+b)\ge 1-\xi_i,\;\;i=1,2,...,n\\ &\xi_i\ge0,\;\;i=1,2,...,n \end{align*} \tag{7}$$

其中，$C\gt0$ 称为惩罚参数，$C$ 值大时对误分类的惩罚增大，$C$ 值小时对误分类的惩罚减小。用于调和两者的系数，我们希望求解$(7)$得到最大间隔划分超平面所对应的模型：

$$f(x)=\omega^Tx+b \tag{8}$$

其中 $\omega$ 和 $b$ 是模型的参数，虽然能够直接使用现成的优化计算包求解，但是我们可以使用更加高效的方法，就是使用拉格朗日乘子法得到其“对偶问题”。

对偶问题

对于式$(8)$每条约束添加拉格朗日乘子$\alpha_i\ge0, \mu_i\ge0$，那么该问题的拉格朗日函数可写为：

$$L(\omega,b,\xi,\alpha,\mu)=\frac{1}{2}\parallel\omega\parallel^2+C\sum_{i=1}^n\xi_i+ \sum_{i=1}^{n}\alpha_i(1-\xi_i-y_i(\omega^Tx_i+b))-\sum_{i=1}^n\mu_i\xi_i \tag{9}$$

考虑函数：

$$\theta_P(x)=\max_{\alpha\ge0,\mu\ge0}L(\omega,b,\xi,\alpha,\mu)\tag{10}$$

其中 $P$ 为原始问题，如果存在某个 $\xi_i\lt0$，那么可令其对应的 $\mu_i\rightarrow +\infty$ 使得 $\theta_P(x)\rightarrow +\infty$，如果存在某个 $x_i$ 和 $\xi_i$ 使得 $1-\xi_i-y_i(\omega^Tx_i+b)\gt0$，那么可令其对应的 $\alpha_i\rightarrow +\infty$ 使得 $\theta_P(x)\rightarrow +\infty$，此有：

$$\theta_P(x)= \begin{cases} f(x),\;\;x满足原始问题约束\\ +\infty,\;\;其他\tag{11} \end{cases}$$

上述式子说明了如果满足约束，最大化问题和原始问题是一致的。

所以如果再考虑极小化问题

$$\min_{\omega,b,\xi}\theta_P(x)=\min_{\omega,b,\xi}\max_{\alpha\ge0,\mu\ge0}L(\omega,b,\xi,\alpha,\mu)\tag{12}$$

他与原始问题$(7)$是等价的。

原命题将转化为一个$p$*的问题：

$$\begin{align*} \min_{\omega,b,\xi}\;&\frac{1}{2} \parallel \omega \parallel^2+C\sum_{i=1}^n\xi_i\\ &=\min_{\omega,b,\xi}{\theta_P(x)},x满足原始问题约束\\ &=\min_{\omega,b,\xi}{\max_{\alpha\ge0,\mu\ge0}{L(\omega,b,\xi,\alpha,\mu)}} = p^* \end{align*} \tag{13}$$

但其实这仍然是一个很难解决的问题，因为我们要先解决含有不等式约束 $\alpha$ 的最大化问题，然后再在 $x$ 上求最小值。如果能将其转化为先求 $x$ 上的最小值，再解决关于 $\alpha$ 的不等式约束的最大化问题就比较简单，即 $d$*

$$\min_{\alpha\ge0,\mu\ge0}{\max_{\omega,b,\xi}{L(\omega,b,\xi,\alpha,\mu)}} = d^* \tag{14}$$

$d$* 就是 $p$* 的对偶性问题，但是常规情况下 $d$*$\le$$p$*，这叫弱对偶性质(Week Duality)，举个真实的栗子方便记忆：

$$\begin{align*} if\ f(x,y)=sin(x+y) \\ \min_{y}{\max_{x}{f(x,y)}} &= -1 \\ \max_{x}{\min_{y}{f(x,y)}} &= 1 \\ if\ f(x,y)=sin(x)+sin(y) \\ \min_{y}{\max_{x}{f(x,y)}} &=\max_{x}{\min_{y}{f(x,y)}}= 0 \\ thus, we\ have\ d^*\le p^* \end{align*} \\\tag{15}$$

对偶间隙 $d$* $-$ $p$* 在满足$Slater$定理的时候间隙会消失，使$d$* $=$ $p$*，即强对偶性质(strong Duality)。根据这篇文章即

1. 原始问题是凸函数
2. 约束条件是线性约束
3. 满足KKT条件

是故原问题将转化为其对偶问题：

$$\begin{align*} \min_{\omega,b,\xi}&\frac{1}{2} \parallel \omega \parallel^2+C\sum_{i=1}^n\xi_i\\ &=\min_{\omega,b}{\max_{\alpha}{L(\omega,b,\xi,\alpha,\mu)}} = p^* \\ &=\max_{\alpha}{\min_{\omega,b}{L(\omega,b,\xi,\alpha,\mu)}} = d^* \\ s.t\ &\sum_{i=1}^{n}a_iy_i=0 \\ & 0\le a_i\le C, \ i=1,2,..,n \end{align*} \tag{16}$$

首先优化内部的拉格朗日方程：

$$L(\omega,b,\xi,\alpha,\mu)=\frac{1}{2}\parallel\omega\parallel^2+C\sum_{i=1}^n\xi_i+ \sum_{i=1}^{n}\alpha_i(1-\xi_i-y_i(\omega^Tx_i+b))-\sum_{i=1}^n\mu_i\xi_i \tag{17}$$

令$L(\omega,b,\xi,\alpha,\mu)$对 $\omega$ 、 $b$ 和 $\xi$ 的偏导为零可得到：

$$\frac{\partial L}{\partial \omega}=\omega-\sum_{i=1}^{m}a_iy_ix_i=0 \Rightarrow \omega=\sum_{i=1}^{m}a_iy_ix_i \\ \tag{18}$$ $$\frac{\partial L}{\partial b}=0 \Rightarrow \sum_{i=1}^{m}a_iy_i=0 \tag{19}$$ $$\frac{\partial L}{\partial \xi}=0\Rightarrow C-\alpha_i-\mu_i=0\tag{20}$$

注意上式的 $m$ 是样本数量而不是特征维度，第 $i$ 个样本的 $x=(x_1;x_2,…,x_d)$，$d$ 才是样本特征的维度。

将$(18)$、$(19)$和$(20)$代入$(17)$得

$$\begin{align*} \min_{\omega,b,\xi}{L(\omega,b,\xi,\alpha,\mu)} =&\frac{1}{2}\parallel\omega\parallel^2+C\sum_{i=1}^n\xi_i+ \sum_{i=1}^{n}\alpha_i(1-\xi_i-y_i(\omega^Tx_i+b))-\sum_{i=1}^n\mu_i\xi_i\\ =&\frac{1}{2}\sum_{i=1}^{m}a_iy_ix_i\sum_{j=1}^{m}a_jy_jx_j+\sum_{i=1}^{m}\alpha_i(1-y_i(\sum_{j=1}^{m}a_jy_jx_j)^Tx_i+b)) \\ =&\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}a_ia_jy_iy_jx_i^Tx_j+\sum_{i=1}^{m}\alpha_i-\sum_{i=1}^{m}\sum_{j=1}^{m}a_ia_jy_iy_jx_i^Tx_j+\sum_{i=1}^{m}\alpha_iy_ib \\ =&\sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}a_ia_jy_iy_jx_i^Tx_j \end{align*} \tag{21}$$

分析式$(15)$，其中$\alpha=(\alpha_1;\alpha_2;...;\alpha_m)\ge0$，而 $1-y_i(\omega^Tx_i+b))\le0$，所以对于后面这一项$\sum_{i=1}^{m}\alpha_i(1-y_i(\omega^Tx_i+b))$的最大值为 $0$，为了最小化该拉格朗日方程，因此要令$\alpha$尽可能地大，所以再对 $\min_{\omega,b,\xi}{L(\omega,b,\xi,\alpha,\mu)}$ 求 $\alpha$ 的极大，即得对偶问题：

$$\begin{align*} \max_{\alpha}&\;L(\omega,b,\xi,\alpha,\mu)=\sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}a_ia_jy_iy_jx_i^Tx_j \\ s.t.&\;\sum_{i=1}^m\alpha_iy_i=0\\ &C-\alpha_i-\mu_i=0\\ &\alpha_i\ge0,\;\;\mu_i\ge0,\;\;i=1,2,...,n \end{align*} \tag{22}$$

利用约束等式消去 $\mu_i$，从而留下最终约束 $\alpha_i$，约束变为 $0\le\alpha_i\le C$。

SMO算法

上述问题为求解凸二次规划问题，这样的问题具有全局最优解，但是由于当训练样本容量很大时，现在的最优化算法往往非常低效，因此使用序列最小最优化算法(sequential minimal optimization, SMO)来求解这个问题，这是一种启发式的算法。SMO每次选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变得更小。更重要的是，这是子问题可以通过解析方法求得，这样就可以大大提高整个算法的计算速度。子问题有两个变量，一个是违反KKT条件最严重的哪一个，另一个由约束条件自动确定。如此，SMO算法将原问题不断分解为子问题并对子问题求解，进而达到求解原问题的目的。其包括两个部分：求解两个变量二次规划的解析方法和选择变量的启发式方法。

两个变量二次规划的求解方法

对于SVM我们优化下述问题：

$$\begin{align*} \min_{\alpha}&\;L(\omega,b,\alpha)=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}a_ia_jy_iy_jK(x_i,x_j) -\sum_{i=1}^{n}\alpha_i\\\ s.t.&\;\sum_{i=1}^n\alpha_iy_i=0\\ &\;0\le\alpha_i\le C,\;\;i=1,2,...,n \end{align*} \tag{23}$$

其中 $K(x_i,x_j)$ 为核函数。

那么SMO的最优化问题的子问题可以写成：

$$\begin{align*} \min_{\alpha_1,\alpha_2}W(\alpha_1,\alpha_2)= \frac{1}{2}(\alpha_1y_1\alpha_1y_1K_{11} +\alpha_2y_2\alpha_2y_2K_{22} +2\alpha_1y_1\alpha_2y_2K_{12}\\ +2\sum_{i=3}^n \alpha_1y_1\alpha_iy_iK_{1i} +2\sum_{i=3}^n \alpha_2y_2\alpha_iy_iK_{2i} +\sum_{i=3}^n\sum_{j=3}^n\alpha_iy_i\alpha_jy_jK_{ij})-(\alpha_1+\alpha_2+\sum_{i=3}^n\alpha_i) \end{align*} \tag{24}$$

其中 $\sum_{i=3}^n\sum_{j=3}^n\alpha_iy_i\alpha_jy_jK_{ij})$ 和 $\sum_{i=3}^n\alpha_i$ 为常数项，所以子问题可以简化为：

$$\begin{align*} \min_{\alpha_1,\alpha_2}W(\alpha_1,\alpha_2)= \frac{1}{2}\alpha_1^2y_1^2K_{11} &+\frac{1}{2}\alpha_2^2y_2^2K_{22} +\alpha_1y_1\alpha_2y_2K_{12} \\ &+\alpha_1y_1\sum_{i=3}^n \alpha_iy_iK_{1i} +\alpha_2y_2\sum_{i=3}^n \alpha_iy_iK_{2i} -(\alpha_1+\alpha_2)\\ s.t.\;\;&\alpha_1y_1+\alpha_2y_2=-\sum_{i=3}^ny_i\alpha_i=\zeta \\ &0\le\alpha_i\le C,\;\;i=1,2 \end{align*} \tag{25}$$

因为 $y_1=1$ 或 $-1$，由约束 $\alpha_1y_1+\alpha_2y_2=C$ 得：

$$\begin{align*} \alpha_1y_1=(\zeta-\alpha_2y_2)\\ \alpha_1=y_1(\zeta-\alpha_2y_2) \end{align*} \tag{26}$$

将该式带入式 $(21)$，并消去 $y_i^2$，得：

$$\begin{align*} W(\alpha_2)= \frac{1}{2}(\zeta-\alpha_2y_2)^2K_{11} &+\frac{1}{2}\alpha_2^2K_{22} +(\zeta-\alpha_2y_2)\alpha_2y_2K_{12} \\ &+(\zeta-\alpha_2y_2)\sum_{i=3}^n\alpha_iy_iK_{1i} +\alpha_2y_2\sum_{i=3}^n\alpha_iy_iK_{2i} -y_1(\zeta-\alpha_2y_2)-\alpha_2 \end{align*} \tag{27}$$

进行求导得：

$$\begin{align*} \frac{\partial W}{\partial\alpha_2} =-y_2(\zeta-\alpha_2y_2)K_{11} &+\alpha_2K_{22} +(\zeta-2\alpha_2y_2)y_2K_{12} \\ &-y_2\sum_{i=3}^n\alpha_iy_kK_{1i} +y_2\sum_{i=3}^n\alpha_iy_iK_{2i}+y_1y_2-1=0 \end{align*} \tag{25}$$

整理上式得：

$$\begin{align*} \alpha_2(K_{11}+K_{22}-2K_{12}) &=\zeta y_2K_{11} -\zeta y_2K_{12} +y_2\sum_{i=3}^n\alpha_iy_kK_{1i} -y_2\sum_{i=3}^n\alpha_iy_iK_{2i} +1-y_1y_2\\ &=y_2(\zeta K_{11}-\zeta K_{12}+\sum_{i=3}^n\alpha_iy_kK_{1i}-\sum_{i=3}^n\alpha_iy_iK_{2i}+y_2-y_1) \end{align*}\tag{26}$$

因为 $\alpha_i$ 更新前后都要满足约束$\varsigma=\alpha_1y_1+\alpha_2y_2$，所以将$\varsigma=\alpha^{old}_1y_1+\alpha_2^{old}y_2$ 代入式 $(26)$ 得：

$$\begin{align*} \alpha_2^{new,unc}(K_{11}+K_{22}-2K_{12}) &=y_2(\zeta K_{11}-\zeta K_{12}+\sum_{i=3}^n\alpha_iy_iK_{1i}-\sum_{i=3}^n\alpha_iy_iK_{2i}+y_2-y_1)\\ &=y_2(\alpha^{old}_1y_1K_{11}+\alpha_2^{old}y_2K_{11}-\alpha^{old}_1y_1K_{12}-\alpha_2^{old}y_2K_{12}\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;+(\sum_{i=1}^n\alpha_iy_iK_{1i}-y_1-\alpha_1^{old}y_1K_{11}-\alpha_2^{old}y_2K_{12})\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;-(\sum_{i=1}^n\alpha_iy_iK_{2i}-y_2-\alpha_1^{old}y_1K_{12}-\alpha_2^{old}y_2K_{22}))\\ &=y_2((K_{11}+K_{22}-2K_{12})\alpha_2^{old}y_2 +(\sum_{i=1}^n\alpha_iy_iK_{1i}-y_1) -(\sum_{i=1}^n\alpha_iy_iK_{2i}-y_2)) \end{align*} \tag{28}$$

令$\mu=K_{11}+K_{22}-2K_{12}=||\Phi(x_1)-\Phi(x_2)||,\;E_j=\sum_{i=1}^n\alpha_iy_iK_{1i}-y_j$ ，其中$\Phi(x)$ 是输入空间到特征空间的映射，得：

$$\alpha_2^{new,unc}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{\mu} \tag{29}$$

上式是最优化问题 $(21)$ 沿着约束方向未经剪辑即未考虑不等式约束时 $\alpha_2$ 的最优解 $\alpha_2^{new,unc}$；然后再求剪辑后 $\alpha_2$ 的解 $\alpha_2^{new}$：

$$a_2^{new}= \begin{cases} H,&a_2^{new,unc}\gt H\\ a_2^{new,unc},&L\le\alpha_2^{new,unc}\le H\\ L,&\alpha_2^{new,unc}\lt L \end{cases} \\ \tag{30} \begin{align*} &L=\max{(0,\alpha_2^{old}-\alpha_1^{old})},\;\;&&H=\min{(C,C+\alpha_2^{old}-\alpha_1^{old})}\;\;&if\;y_1\ne y_2\\ &L=\max(0,\alpha_2^{old}+\alpha_1^{old}-C),\;\;&&H=\min(C,\alpha_2^{old}+\alpha_1^{old})\;\;&if\;y_1=y_2\\ 或者写成：\\ &L=\max(0,-k)\;\;&&H=\min(C,C-k)\;\;&if\;y_1\ne y_2\\ &L=\max(0,k-C)\;\;&&H=\min(C,k)\;\;&if\;y_1=y_2 \end{align*}$$

由 $\alpha_2^{new}$ 求得 $\alpha_1^{new}$ 的解为

$$\alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new})\tag{31}$$

变量的选择方法

令 $g(x)$为分离超平面

$$g(x)=\sum_{i=1}^n\alpha_iy_iK(x_i,x)+b \tag{32}$$

检验训练样本点 $(x_i, y_i)$ 是否满足 KKT 对偶互补条件，即：

$$\begin{align*} \alpha_i(y_i(\omega x_i+b)-1+\xi_i)=0\\ \end{align*} \tag{33}$$

已知的约束有：

$$\begin{align*} C-\alpha_i-\mu_i=0\\ \mu_i\xi_i=0\\ y_i(\omega x_i+b)-1+\xi_i\ge0 \end{align*} \tag{34}$$

• 如果 $\alpha_i=0$ ，则有 $\mu_i=C,\;\xi_i=0,g(x_i)\ge1$，即样本在支持向量上或者已经被正确分类。
• 如果 $0\lt\alpha_i\lt C$，则有 $0\lt\mu_i\lt C,\;\xi_i=0,\;g(x_i)=1$ ，此时样本在支持向量上。
• 如果$\alpha_i=C$，则有$\mu_i=0,\;\xi_i\ge0,\;g(x_i)\le1$，此时样本在支持向量与分类边界之间。

SMO算法称选择第一个变量为外层循环，这个变量需要选择在训练集中违反KKT条件最严重的样本点。具体地，检验训练样本点 $(x_i,y_i)$是否满足KKT条件，即：

$$\begin{align*} \alpha_i^*=0 \Leftrightarrow y_ig(x_i)\ge1\\ 0\lt\alpha_i^*\lt C\Leftrightarrow y_ig(x_i)=1\\ \alpha_i^*=C\Leftrightarrow y_ig(x_i)\le1 \end{align*} \tag{35}$$

一般来说，首先选择违反 $0\lt\alpha_i^*\lt C\Leftrightarrow y_ig(x_i)=1$ 这个条件的点。如果这些支持向量都满足KKT条件，再选择违反 $\alpha_i^*=0 \Leftrightarrow y_ig(x_i)\ge1$ 和 $\alpha_i^*=C\Leftrightarrow y_ig(x_i)\le1$ 的点。

SMO算法称选择第二个变量为内层循环，假设在外层循环中已经找到第一个变量 $\alpha_1$，现在要在内层循环中找到第二个变量 $\alpha_2$。第二个变量选择的标准是希望能使 $\alpha_2$ 有足够大的变化。由 $(29)$ 知，$a_2^{new}$ 是依赖 $|E_1-E_2|$ 的，为了加快计算速度，一种简单的做法是选择 $\alpha_2$，使其对应的$|E_1-E_2|$最大。因为，$\alpha_1$ 和 $E_1$ 已经确定。如果 $E_1$ 是正的，那么选择最小的 $E_i$ 作为 $E_2$；如果 $E_1$ 是负的，那么选择最大的 $E_1$ 作为 $E_2$。为了节省计算时间，将所有 $E_i$ 值保存在一个列表中。

在特殊情况下，如果内层循环通过以上方法选择的 $\alpha_2$ 不能使目标函数有足够的下降，那么采用以下启发式规则继续选择 $\alpha_2$。遍历在间隔边界上的支持向量，依次将其对应的变量作为 $\alpha_2$ 试用，知道目标函数有足够的下降。若找不到合适的 $\alpha_2$，那么遍历训练数据集；若仍找不到合适的 $\alpha_2$，则放弃第一个 $\alpha_1$， 再通过外层循环寻求另外的 $\alpha_1$。

对于阈值 $b$ 和差值 $E_i$，在每次完成两个变量的优化后，都要重新计算阈值 $b$。当 $0\lt\alpha_1^{new}\lt C$，由KKT条件$(35)$可知：

$$\sum_{i=1}^n\alpha_iy_iK_{i1}+b=y_1 \tag{36}$$

于是

$$b_1^{new}=y_i-\sum_{i=3}^n\alpha_iy_iK_{i1}-\alpha_1^{new}y_1K_{11}-\alpha_2^{new}y_2K_{21} \tag{37}$$

由 $E_1$ 的定义式有

$$E_1=\sum_{i=3}^n\alpha_iy_iK_{i1}+\alpha_1^{old}y_1K_{11}+\alpha_2^{old}y_2K_{21}+b^{old}-y_1 \tag{38}$$

用 $(38)$ 式的

$$y_1-\sum_{i=3}^n\alpha_iy_iK_{i1}=-E_i+\alpha_1^{old}y_1K_{11}+\alpha_2^{old}y_2K_{21}+b^{old}\tag{39}$$

消去 $(37)$ 式的前两项得：

$$\begin{align*} b_1^{new}&=-E_i+\alpha_1^{old}y_1K_{11}+\alpha_2^{old}y_2K_{21}+b^{old}-\alpha_1^{new}y_1K_{11}-\alpha_2^{new}y_2K_{21}\\ &=-E_1-y_1K_{11}(\alpha_1^{new}-\alpha_1^{old})-y_2K_{21}(\alpha_2^{new}-\alpha_2^{old})+b^{old} \end{align*} \tag{40}$$

同样，如果 $0\lt\alpha_2^{new}\lt C$，那么

$$b_2^{new}=-E_2-y_1K_{12}(\alpha_2^{new}-\alpha_2^{old})-y_2K_{22}(\alpha_2^{new}-\alpha_2^{old})+b^{old} \tag{41}$$

最终的 $b^{new}$ 为：

$$b^{new}=\frac{b_1^{new}+b_2^{new}}{2} \tag{42}$$

在每次完成两个变量的优化后，还必须更新其对应的 $E_i$ 值，并将它们保存在列表中。 $E_i$ 值的更新要用到 $b^{new}$ 以及所有支持向量对应的 $\alpha_j$：

$$E_i^{new}=\sum_Sy_j\alpha_jK(x_i,x_j)+b^{new}-y_i$$

其中 $S$ 是所有支持向量的集合。

总的来说SMO算法流程如下：

拉格朗日乘子法

拉格朗日对偶性相关知识是李航《统计机器学习》的内容，而对于拉格朗日乘子法几何意义，主要是网上的解释，我认为解释的比较生动的是马同学的解释，总结的比较精炼的是卢健龙的回答，当然两篇都是来自同一个知乎的帖子。

原始问题

假设$f(x), c_i(x), h_j(x)$是定义在 $\text{R}^n$ 上的连续可微函数。考虑约束最优化问题：

$$\begin{align*} \min_{x\in \text{R}^n}&\;f(x)\\ s.t.\;\;&c_i(x)\le0,\;\;i=1,2...,k\\ &h_j(x)=0,\;\;j=1,2,...,l \end{align*} \tag{*1}$$

将此称为最优化问题为原始最优化问题或原始问题。

首先，引入广义拉格朗日函数

$$L(x,\alpha,\beta)=f(x)+\sum_{i=1}^k\alpha_ic_i(x)+\sum_{j=1}^l\beta_jh_j(x) \tag{*2}$$

这里，$x=(x^{(1)},x^{(1)},...x^{(n)})^T\in\text{R}^n,\alpha_i,\beta_j$是拉格朗日乘子，$\alpha_i\ge0$。考虑 $x$ 的函数：

$$\theta_P(x)=\max_{\alpha,\beta;\alpha_i\ge0}L(x,\alpha,\beta) \tag{*3}$$

这里，下标 $P$ 表示原始问题。

假设给定某个 $x$。如果 $x$ 违反原始问题的约束条件，即存在某个 $i$ 使得 $c_i(x)\gt0$ 或者存在某个 $j$ 使得 $h_j(x) \ne 0$，那么有

$$\theta_P(x)=\max_{\alpha,\beta;\alpha_i\ge0}[f(x)+\sum_{i=1}^k\alpha_ic_i(x)+\sum_{j=1}^j\beta_jh_j(x)]=+\infty \tag{*4}$$

因为若某个 $i$ 使得约束 $c_i(x)\gt0$ ，则可令 $\alpha_i\rightarrow+\infty$ 使得 $\alpha_ic_i(x)\rightarrow +\infty$；若某个 $j$ 使 $h_j(x)\ne0$, 则可令 $\beta_j$ 使 $\beta_j h_j(x) \rightarrow +\infty$，而将其余各 $\alpha_i,\beta_j$ 均取为0。

相反地，如果 $x$ 满足约束条件，则有

$$\theta_P(x)=\begin{cases} f(x),\;x满足原始问题约束\\ +\infty,\;其他 \end{cases} \tag{*5}$$

所以如果考虑极小化问题

$$\min_x\theta_P(x)=\min_x\max_{\alpha,\beta;\alpha_i\ge0}L(x,\alpha,\beta) \tag{*6}$$

它是与原始最优化问题等价的，即它们有相同的解。

该问题称为广义拉格朗日函数的极小极大问题。这样一来，就把原始最优化问题表示为广义拉格朗日函数的极小极大问题。为了方便，定义原始问题的最优值

$$p^*=\min_x\theta_P(x) \tag{*7}$$

称为原始问题的值。

对偶问题

定义

$$\theta_D(\alpha, \beta)=\min_xL(x,\alpha,\beta) \tag{*8}$$

再考虑极大化 $\theta_D(\alpha, \beta)=\min_xL(x,\alpha,\beta)$, 即

$$\max_{\alpha,\beta;\alpha\ge0}\theta_D(\alpha,\beta)=\max_{\alpha,\beta;\alpha_i\ge0}\min_xL(x,\alpha,\beta) \tag{*9}$$

问题 $\max_{\alpha,\beta;\alpha_i\ge0}\min_xL(x,\alpha,\beta)$ 称为广义拉格朗日函数的极大极小问题。

可以将广义拉格朗日函数的极大极小问题表示为约束最优化问题：

$$\begin{align*} \max_{\alpha,\beta}\theta_D(\alpha,\beta)=\max_{\alpha,\beta}\min_xL(x,\alpha,\beta)\\ s.t.\;\alpha_i\ge0,\;\;i=1,2,...,k \end{align*} \tag{*10}$$

称为原始问题的对偶问题。定义对偶问题的最优值

$$d^*=\max_{\alpha,\beta;\alpha_i\ge0}\theta_D(\alpha,\beta) \tag{*11}$$

称为对偶问题的值。

原始问题和对偶问题的关系

定理：若原始问题和对偶问题都有最优值，则

$$d^*=\max_{\alpha,\beta;\alpha_i\ge0}\min_xL(x,\alpha,\beta)\le\min_x\max_{\alpha,\beta;\alpha_i\ge0}L(x,\alpha,\beta)=p^* \tag{*12}$$

推论：假设函数 $f(x)$ 和 $c_i(x)$ 是凸函数（不等式约束），$h_j(x)$ 是仿射函数（等式约束）；并且假设不等式约束 $c_i(x)$ 是严格可行的，即存在 $x$ 对所有 $i$ 又 $c_i(x)\lt0$，则存在 $x^*, \alpha^*, \beta^*$ 使$x^*$ 是原始问题的解，$\alpha^*,\beta^*$ 是对偶问题的解，并且：

$$p^*=d^*=L(x^*,\alpha^*,\beta^*) \tag{*13}$$

且其充分必要条件是$x^*, \alpha^*, \beta^*$满足KKT条件：

$$\begin{align*} \nabla_xL(x^*, \alpha^*, \beta^*)=0\\ a^*_ic_i^*(x^*)=0\;\;i=1,2,...,k\\ c_i(x^*)\le0,\;\;i=1,2,...,k\\ a_i^*\ge0,\;\;i=1,2,...,k\\ h_j(x^*)=0\;\;j=1,2,...,l \end{align*} \tag{*14}$$

几何意义

拉格朗日乘子法具有很直观的几何意义。

单约束情况

比如在给定函数$f(x,y)=x^2y-3$找到曲线上距离原点最近的点，其可以转化为

$$\begin{align*} &\min_{x,y}x^2+y^2 \\ &s.t. \ \ \ \ x^2y-3=0 \end{align*}\tag{*15}$$

（图来自马同学)可以看成一个圆心为原点半径逐渐增大的圆上寻找一个与曲线$f(x,y)=x^2y-3的$交点，不难发现圆上通过该交点的切线也将相切于曲线$f(x,y)=x^2y-3$

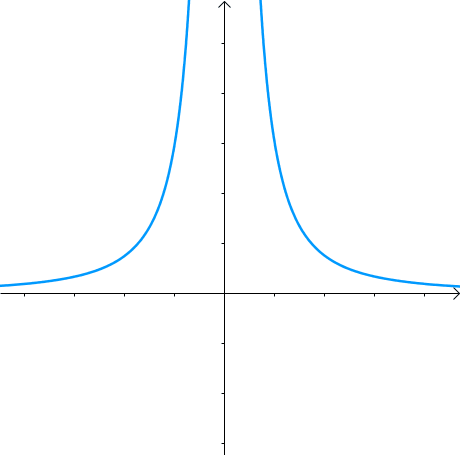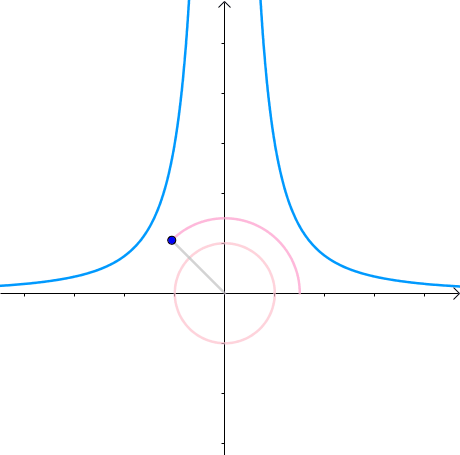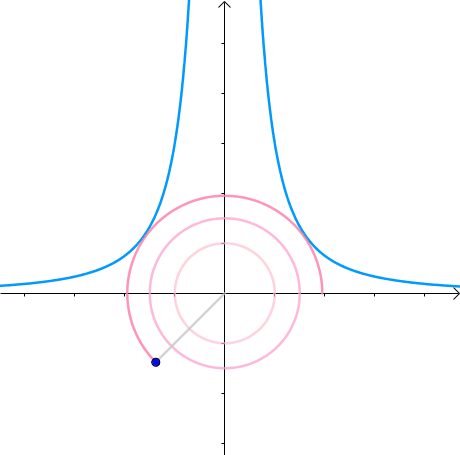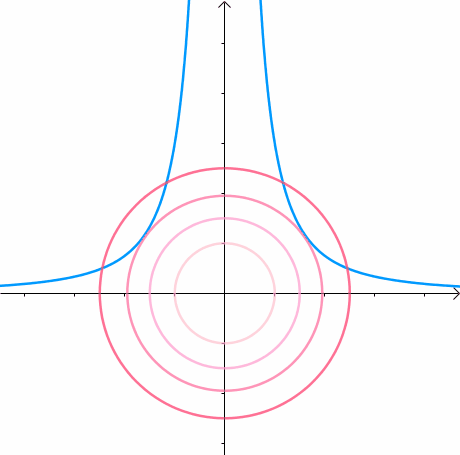
从另一个角度来看，目标函数在取得极值的时候，其极值点的梯度向量的方向与约束函数的在该极值点的梯度方向是一致（平行）的，也就是

$$\nabla g= \lambda \nabla f \tag{*16}$$

其中$ g(x,y)=x^2y-3，f(x,y)=x^2+y^2$，$\nabla g=\binom{\frac{\partial g}{\partial x}}{\frac{\partial g}{\partial y}}=\binom{2xy}{x^2}$ ，$\nabla f=\binom{\frac{\partial f}{\partial x}}{\frac{\partial g}{\partial y}}=\binom{2x}{2y}$为了求取目标函数极值点，因此联立方程组

$$\begin{cases} \nabla g= \lambda \nabla f \\ x^2y-3=0 \end{cases} \Rightarrow \begin{cases} \binom{2x}{2y}=\lambda \binom{2xy}{x^2} \\ x^2y-3=0 \end{cases} \Rightarrow \begin{cases} x\approx\pm1.61 \\ y\approx1.1 \\ \lambda\approx0.87 \end{cases} \tag{*17}$$

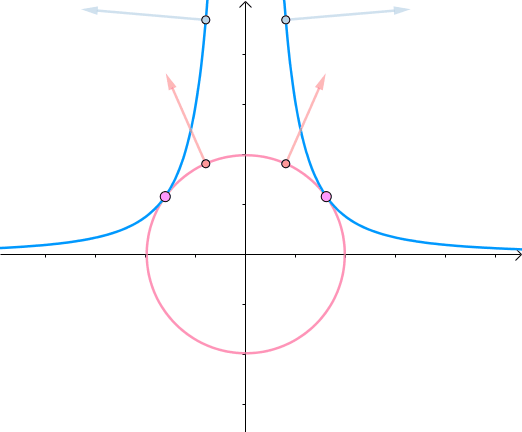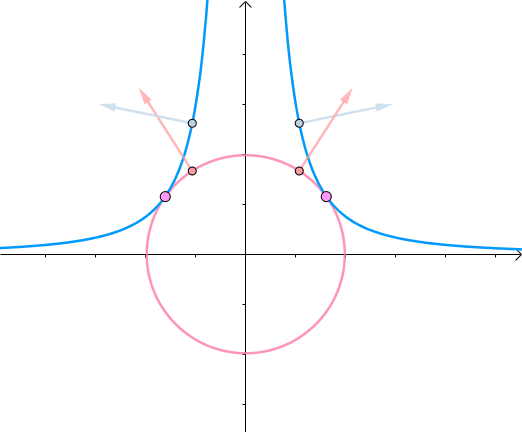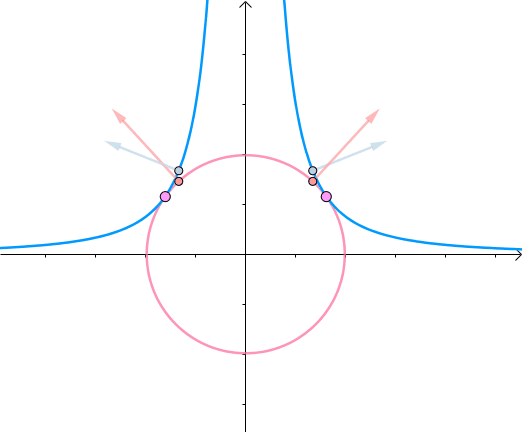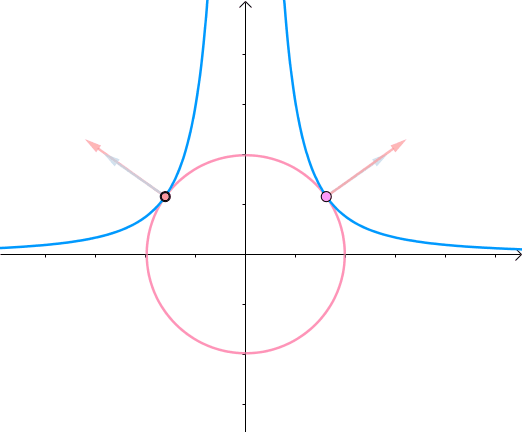
多约束情况

上面说的是单约束的情况下，而在多约束的情况下

$$\begin{align*} \min_{x,y}x^2+y^2 \\ s.t \begin{cases} x^2y-3=0 \\ x-y-3=0 \end{cases} \end{align*} \tag{*18}$$

那么情况就会变成下图

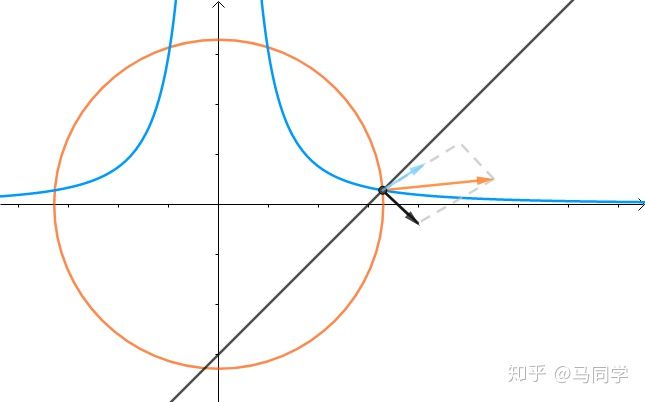
即$x^2 + y^2$的法线是是$x^2y-3$和$x-y-3$的法线的线性组合：

如果

$$\begin{cases} f(x,y)=x^2+y^2 \\ g(x,y)=x^2y-3 \\ h(x,y)=x-y-3 \end{cases} \tag{*19}$$

那么线性组合

$$\nabla f= \lambda \nabla g+\mu \nabla h \tag{*20}$$

联立方程

$$\begin{cases} \nabla f= \lambda \nabla g+\mu \nabla h \\ g(x,y)=0 \\ h(x,y)=0 \end{cases} \tag{*21}$$

即可进行求解.

也就是说在等式约束的优化问题中，假定$x$为$d$维向量，给定目标函数$f(x)$以及约束$g(x)=0,h(x)$，寻找$x$的某个取值$x$*使得目标函数最小化（最大化问题可以通过倒数转化为最小化问题），在最优点$x$*处，梯度$\nabla f(x)$和梯度$\nabla g(x)$和$\nabla h(x)$的线性组合的方向必定相同或相反，即存在$\lambda\ne0, \mu\ne0$使得

$$\nabla f(x^*) + \lambda \nabla g(x^*)+\mu\nabla h(x^*) = 0 \tag{*22}$$

$\lambda,\mu$称为拉格朗日乘子，定义拉格朗日函数

$$L(x, \lambda, \mu)=f(x)+\lambda g(x)+\mu h(x) \tag{*23}$$

将其对$x$的偏导数$\frac{\partial L}{\partial x}=0$可以得到式$(*9)$，将其对$\lambda$的偏导数$\frac{\partial L}{\partial \lambda}=0$即能得到约束条件$g(x)=0$，其对$\mu$的偏导数$\frac{\partial L}{\partial\lambda}=0$即能得到约束条件$h(x)=0$，从而将原约束优化问题转化为对拉格朗日函数$L(x,\lambda)$的无约束优化问题。

KKT条件

考虑下述不等式约束问题：

$$\begin{align*} \min_x f(x)\\ s.t.\;\;g(x)\le 0 \end{align*} \tag{*24}$$

对应的拉格朗日函数为：

$$L(x,\lambda)=f(x)+\lambda g(x) \tag{*25}$$

此时最优点 $x$*或在$ g(x)<0 $的区域中，或在边界$g(x)=0$上。对于$g(x)\lt0$的情形，约束$g(x)\le0$不起作用，可直接通过条件$\nabla f(x)=0$来获得最优点；这等价于将$\lambda$置零后$L(x, \lambda)$对x求偏导得到最优点，$g(x)=0$得到情形类似于上面等式约束的分析，但值得注意的是，此时$\nabla f(x$*$)$的方向必定与$\nabla g(x$*$)$的方向相反，即存在$\lambda\gt0$使得$\nabla f(x^*)+\lambda \nabla (x^*)=0$。

虽然这段话我抄自西瓜书的附录，但是它给出的图片解释非常有限，因此我又查阅的相关资料，考虑这种情况：

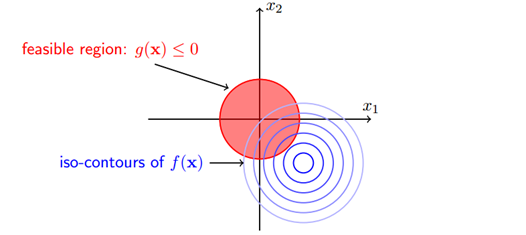
其红色区域代表着约束区域，蓝色是目标函数的等高线，强调这是不等式约束，即要求可行解必须落在约束区域 $g(x)$ 之内，那么由图可见可行解 $x$ 只能在 $g(x)\lt0$ 或者 $g(x)=0$ 的区域内取得，那么会有以下两种情况：

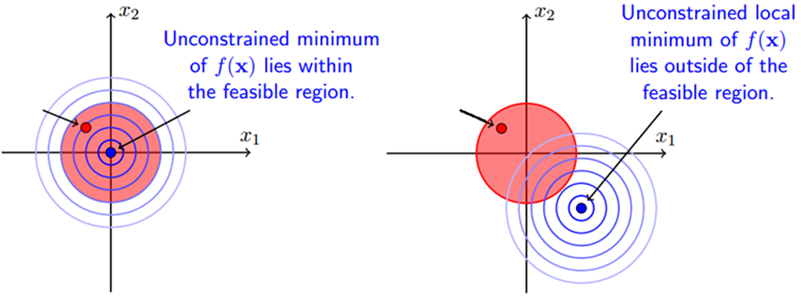
这时候再读上面那句话就可以理解最优点取值的两种情况：

1. 目标函数最优点与约束区域重叠的时候，即极值点 $x$ 落在 $g(x)\lt0$ 的区域内，可以看成将$\lambda$置零后$L(x, \lambda)$对 $x$ 求偏导得到最优点，即直接极小化 $f(x)$ 即可。
2. 目标函数最优点在约束区域之外的时候，即极值点 $x$ 落在 $g(x)=0$ 即边界上，此时等价于等式约束优化问题，那么最优点将在约束边界产生，这将转化为上述等式约束的情况。

用公式表达就是意思就是：

$$\begin{cases} \begin{cases} g(x)<0 \\ \lambda=0 \end{cases} \\ \begin{cases} g(x)=0 \\ \lambda>0 \end{cases} \end{cases} \Rightarrow \begin{cases} g(x)\le0 \\ \lambda\ge0 \\ \lambda g(x)=0, \lambda和g(x)必有一为零 \end{cases} \\ \tag{*26}$$

上述公式的右边称为Karush-Kuhn-Tucker(简称KKT)条件。

还有一个问题是 $\lambda$ 的取值，在等式约束优化中，约束函数与目标函数的梯度只要满足平行即可；而在不等式约束中则不然，若 $\lambda\ne0$，这说明可行解 $x$ 是落在约束区域的边界上的，这是可行解应尽量靠近无约束时的解，所以在约束边界上，目标函数的负梯度方向应该远离约束区域朝向无约束时的解，此时正好可得约束函数的梯度方向与目标函数的负梯度方向应该相同，即$\nabla f(x$*$)$的方向必定与$\nabla g(x$*$)$的方向相反，即存在$\lambda\gt0$使得：

$$\nabla f(x^*)+\lambda\nabla g(x^*)=0 \tag{*27}$$

这个问题可以举一个形象的例子，假设你去爬山，目标是山顶，但有一个障碍挡住了通向山顶的路，所以只能沿着障碍爬到尽可能靠近山顶的位置，然后望着山顶叹叹气，这里山顶便是目标函数的可行解，障碍便是约束函数的边界，此时的梯度方向一定是指向山顶的，与障碍的梯度同向，下图描述了这种情况：”

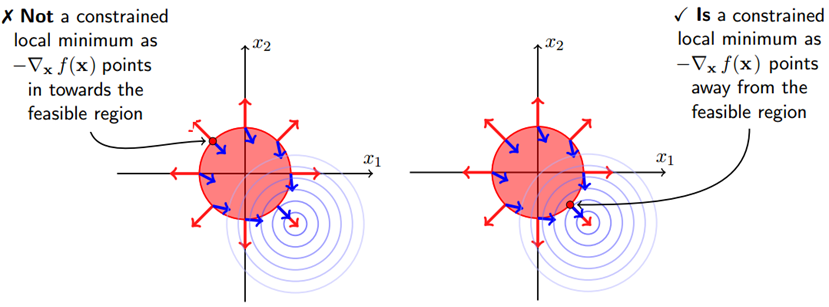
对于不等式约束，只要满足KKT条件，依然可以使用拉格朗日乘子法解决，这个条件便是KKT条件。

参考文献

1. 《机器学习》-周志华
2. 《统计学习方法》-李航
3. https://www.cnblogs.com/xxrxxr/p/7538430.html
4. https://www.cnblogs.com/ooon/p/5721119.html
5. https://www.zhihu.com/question/38586401
6. https://zhuanlan.zhihu.com/p/28804123
7. https://blog.csdn.net/feilong_csdn/article/details/62427148