逗比学长的博客

此人有“亿”点强迫症

ubuntu和windows下运行MPI做埃拉托色尼素数筛选法

发表于 更新于 分类于 阅读次数：

说说最近踩的坑，为了在windows的电脑下做并行程序设计作业埃拉托色尼素数筛选法，用的是MPI，然后发现这类库对于windows的用户非常不友好，比如说MPICH2后续已经不支持windows，OpenMPI貌似只支持linux，而微软维护的MS-MPI能够支持windows，但是我在使用clion(cmake)进行包引入的时候出了很多问题，可能的原因是windows下没有mpicc/mpicxx，可能的解决方案是使用微软自家的VS去做，但是我觉得VS太过臃肿而不想下载，最终我得出来的结论是：windows + clion + MPI 暂时无法实现，即使翻阅了很多网上的资料也没有响应的解决方案，无奈之下只能在远程的linux下编程，使用的是ubuntu 16.04这个系统，然后思路是因为要编程所以配置一个ubuntu GUI，然后装上lion，把之前写的代码从git下clone下来，然后由于我的服务器是在华为云上的一个7天体验卷，也就只有2核4G，所以我打算后续在工作室一台比较老的服务器上写代码，然后比较坑的是那个玩意儿没有公网IP，因此我想看看能否通过teamviewer来从远程连接，虽然感觉可能性不大hhh。

2019-05-19续——

后来我测试了一下teamviewer连接服务器，但是这个被归为了商业用途就是要收费的（就很烦），算了算了…只能老老实实用windows的远程连接8。后续在linux服务器上写完了几个优化之后（见后）,在测试阶段发现优化后的时间反而边长了，虽然后来用了增加cache命中率来提升性能，但是我认为加速还是受到了干扰，于是只能去专业的实验室用里面的电脑搞事情，所以我又把windows上mpi的配置搞了一边，还生成了一下不同优化的exe，然后再拿回自己的电脑测试，现在想一想，之前无法在自己的电脑的windows上用clion编译可能是和cmake建立动态链接失败有关，但是自己对这方面不熟，网上资料不全，所以搞着搞着就放弃了。但是安装了mpi还是能够执行编译生成的exe文件滴。

Linux环境配置

图形界面

安装

我借鉴了这篇博客上的流程

更新软件列表和软件

1
2
sudo apt-get update
sudo apt-get upgrade

安装xrdp

1
sudo apt-get install xrdp

安装vn4server

1
sudo apt-get install vnc4server

安装xubuntu-desktop，这个有点久

1
sudo apt-get install xubuntu-desktop

向xsession中写入xfce4-session

1
echo “xfce4-session” >~/.xsession

开启xrdp服务

1
sudo service xrdp restart

远程登录

使用windows下的远程桌面连接，输入IP，用户名

1

输入密码

2

使用默认设置

3

clion

安装

下载网站找到direct link，将里面的url复制过来下载

1
wget https://download.jetbrains.com/cpp/CLion-2019.1.2.tar.gz

解压

1
tar -zxvf CLion-2019.1.2.tar.gz

安装(图形界面下)

1
2
cd clion-2019.1.2/bin/
./clion.sh

安装完成后进行相关配置即可

缺少c/c++编译器

1
apt-get install gcc g++

teamviewer

安装

下载网站找到TeamViewer Host的ubuntu 64x地址复制过来下载

1
wget https://download.teamviewer.com/download/linux/teamviewer-host_amd64.deb

安装deb软件包

1
sudo dpkg -i teamviewer-host_amd64.deb

修复安装

1
apt-get -f install

直接执行teamviewer应该是会报错的，报的是Aborted (core dumped)，正确的做法应该是

查看配置

1
teamviewer info

其将打印出TeamViewer ID

4

通过下属命令设置登录密码

1
teamviewer --passwd NEWPASSWORD

打印 ok，在其他电脑上下载TeamViewer客户端，即可进行远程控制，若不行可以进行服务器重启再试试。

然鹅，这样貌似会触碰到TeamViewer的商业用途，奥

5

MPICH

安装

1
sudo apt-get install mpich

CMakeLists.txt下配置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
cmake_minimum_required(VERSION 3.13)
project(MPI)

set(CMAKE_CXX_STANDARD 17)


find_package(MPI REQUIRED)

include_directories(${MPI_INCLUDE_PATH})

set(CMAKE_CXX_COMPILER mpicxx)
set(CMAKE_C_COMPILER mpicc)

add_executable(MPI main.cpp)

测试代码

来自这个博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include "mpi_hello.h"
#include "cstdio"
#include "cstring"
#include "mpi.h"
 
const int MAX_STRING = 100;
 
int main() {
    char greeting[MAX_STRING];
    int comm_sz;
    int my_rank;
 
    MPI_Init(NULL, NULL);
    MPI_Comm_size(MPI_COMM_WORLD, &comm_sz);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
 
    if (my_rank != 0) {
        sprintf(greeting, "Greeting from process %d of %d!", my_rank, comm_sz);
        MPI_Send(greeting, strlen(greeting) + 1, MPI_CHAR, 0, 0, MPI_COMM_WORLD);
    } else {
        printf("Greetings from process %d of %d!\n", my_rank, comm_sz);
        for (int q = 1; q < comm_sz; ++q) {
            MPI_Recv(greeting, MAX_STRING, MPI_CHAR, q, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
            printf("%s\n", greeting);
        }
    }
    MPI_Finalize();
    return 0;
}

运行结果为：

1
2
3
4
5
6
7
/usr/bin/mpirun -np 4 ./mpi_spmv
Greetings from process 0 of 4!
Greeting from process 1 of 4!
Greeting from process 2 of 4!
Greeting from process 3 of 4!
 
Process finished with exit code 0

windows环境配置

windows下运行mpi首推微软的msmpi，因为其配置较mpich更加简单，下载地址为https://docs.microsoft.com/en-us/message-passing-interface/microsoft-mpi

将两个安装包msmpisdk.msi和msmpisetup.exe分别下载然后安装完成后即可。

为啥不按照实验指导书使用mpich，因为用起来太麻烦了！！还要windows的用户和密码，如果没有密码还不行，完了没密码的用户还要创建一个新的用户，而我是在实验室的电脑做的实验，它还不允许我创建新用户，让我心里直呼辣鸡windows，幸好还有MS维护的msmpi，实验才得以进行下去。

关于msmpi的引入我参考了这篇文章，前面说了，仅限于VS，毕竟都是自家的玩意儿引入起来更加方便。

MSMPI配置步骤

  1. 在VS中新建C++win32空项目，将项目编译改为x64（vs总是将这个默认为win32，就很烦)

6

  1. 去安装的SDK目录，找到include与lib文件夹右键项目 — 属性 — vc++ 目录中包含目录添加 include 文件夹路径，库目录中添加 lib 文件夹路径。

7

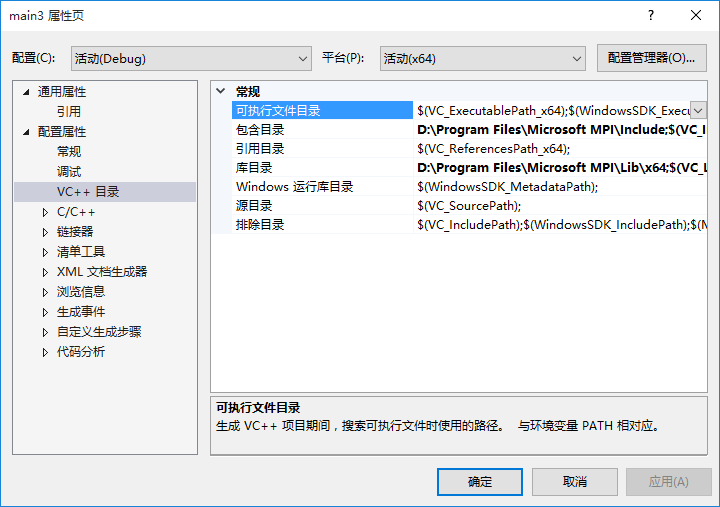
  1. 属性 — 链接器 — 输入 — 附加依赖项中添加msmpi.lib;msmpifec.lib;msmpifmc.lib ;

8

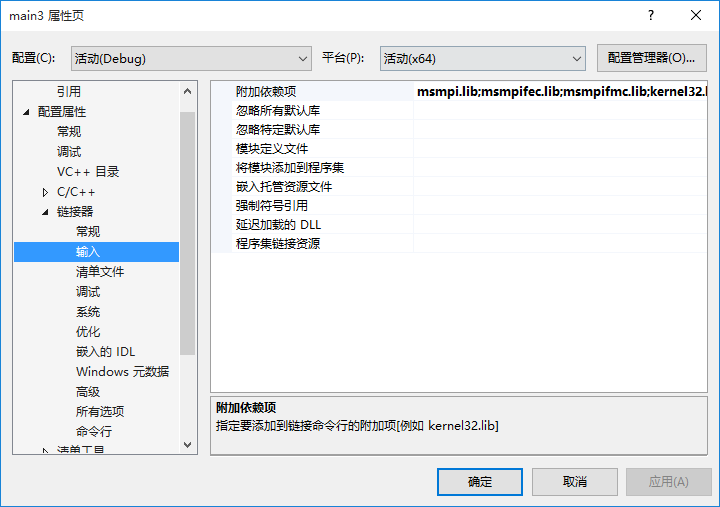
  1. 新建cpp文件，键入测试代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
#include "mpi.h"
#include
int main(int argc, char* argv[])
{
    int rank;
    int size;
    MPI_Init(0,0);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &size);
    std::cout<<"Hello world from process "<<rank<<" of "<<size<<std::endl;
    MPI_Finalize();
    return 0;
}

跳到编译生成exe文件下的目录，执行下列命令，mpiexec刚刚安装bin下的一个执行mpi用的文件，默认配置了系统全局变量，如果没有的话可自行配置

1
mpiexec -n 4 main.exe

得到运行结果如下

1
2
3
4
Hello world from process 1 of 4
Hello world from process 0 of 4
Hello world from process 3 of 4
Hello world from process 2 of 4

至此，windows下的mpi环境配置成功了

埃拉托色尼素数筛选法

原理

根据百度百科介绍，埃拉托色尼筛选法是针对自然数列中的自然数而实施的，用于求一定范围内的质数。

在寻找整数Ｎ以内的素数时，埃拉托斯特尼采用了一种与众不同的方法：先将２－Ｎ的各数写在纸上：

在２的上面画一个圆圈，然后划去２的其他倍数；第一个既未画圈又没有被划去的数是３，将它画圈，再划去３的其他倍数；现在既未画圈又没有被划去的第一个数是５，将它画圈，并划去５的其他倍数……依此类推，一直到所有小于或等于Ｎ的各数都画了圈或划去为止。这时，画了圈的以及未划去的那些数正好就是小于Ｎ的素数。

其伪代码如下所示：

1
2
3
4
5
6
7
Create list of unmarked natural numbers 2, 3, …, n
k <- 2
Repeat
   Mark all multiples of k between k^2 and n
   k<- smallest unmarked number > k
until k^2 > n
The unmarked numbers are primes

初始版并行代码代码说明

定义一个数组marked, 每一个元素的下标对应一个整数，它的值表示这个整数是否为素数,值为1是素数，值为0不是素数。

先假定所有的数都是素数，将marked数组置0。

选定第一个整数２，从它对应的数组元素2*2=4开始依次标记2的倍数，一直标记到最后一个数为止。

接下来选定下一个未标记的数，它一定是素数，在使用广播的形式通知各进程筛选出这个素数的倍数。

这样循环到最后，所有进程中未标记的数之和就是1-n中的所有素数了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
#include "mpi.h"
#include "math.h"
#include "stdio.h"
#include "stdlib.h"
#include "string.h"
#include "error.h"

using namespace std;

/************************************************
MPI_BCAST(buffer,count,datatype,root,comm)
    IN/OUT　buffer　　  通信消息缓冲区的起始地址(可变)
    IN　　　 count　  　 通信消息缓冲区中的数据个数(整型)
    IN 　　　datatype 　通信消息缓冲区中的数据类型(句柄)
    IN　　　 root　  　　发送广播的根的序列号(整型)
    IN 　　　comm   　　通信子(句柄)
int MPI_Bcast(void* buffer,int count,MPI_Datatype datatype,int root, MPI_Comm comm)
MPI_BCAST是从一个序列号为root的进程将一条消息广播发送到组内的所有进程,
包括它本身在内.调用时组内所有成员都使用同一个comm和root,
其结果是将根的通信消息缓冲区中的消息拷贝到其他所有进程中去.
规约函数 MPI_Reduce()，将通信子内各进程的同一个变量参与规约计算，并向指定的进程输出计算结果
MPI_METHOD MPI_Reduce(
   _In_range_(!= , recvbuf) _In_opt_ const void* sendbuf,  // 指向输入数据的指针
   _When_(root != MPI_PROC_NULL, _Out_opt_) void* recvbuf, // 指向输出数据的指针，即计算结果存放的地方
   _In_range_(>= , 0) int count,                           // 数据尺寸，可以进行多个标量或多个向量的规约
   _In_ MPI_Datatype datatype,                             // 数据类型
   _In_ MPI_Op op,                                         // 规约操作类型
   _mpi_coll_rank_(root) int root,                         // 目标进程号，存放计算结果的进程
   _In_ MPI_Comm comm                                      // 通信子
);
**********************************************/
#define MIN(a, b) ((a)<(b)?(a):(b))

int main(int argc, char *argv[]) {
    int count;              /* Local prime count */
    double elapsed_time;    /* Parallel execution time */
    int first;              /* Index of first multiple */
    int global_count;       /* Global prime count */
    int high_value;         /* Highest value on this proc */
    int id;                 /* Process ID number */
    int index;              /* Index of current prime */
    int low_value;          /* Lowest value on this proc */
    char *marked;           /* Portion of 2,...,'n' */
    int n;                  /* Sieving from 2, ..., 'n' */
    int p;                  /* Number of processes */
    int proc0_size;         /* Size of proc 0's subarray */
    int prime;              /* Current prime */
    int size;               /* Elements in 'marked' */
    int low_index;          /* Lowest index on this proc */
    int high_index;         /* Highest index on this proc */

    // 初始化
    // MPI程序启动时“自动”建立两个通信器：
    // MPI_COMM_WORLD:包含程序中所有MPI进程
    // MPI_COMM_SELF：有单个进程独自构成，仅包含自己
    MPI_Init(&argc, &argv);

    // MPI_COMM_RANK 得到本进程的进程号，进程号取值范围为 0, …, np-1
    MPI_Comm_rank(MPI_COMM_WORLD, &id);

    // MPI_COMM_SIZE 得到所有参加运算的进程的个数
    MPI_Comm_size(MPI_COMM_WORLD, &p);

    // MPI_Barrier是MPI中的一个函数接口
    // 表示阻止调用直到communicator中所有进程完成调用
    MPI_Barrier(MPI_COMM_WORLD);

    // MPI_WTIME返回一个用浮点数表示的秒数
    // 它表示从过去某一时刻到调用时刻所经历的时间

    elapsed_time = -MPI_Wtime();

    // 参数个数为2：文件名以及问题规模n
    if (argc != 2) {
        if (!id) printf("Command line: %s <m> \n", argv[0]);
        // 结束MPI系统
        MPI_Finalize();
        exit(1);
    }

    // 表示找 <= n的素数
    n = atoi(argv[1]);

    int N = n - 1;
    low_index = id * (N / p) + MIN(id, N % p); // 进程的第一个数的索引
    high_index = (id + 1) * (N / p) + MIN(id + 1, N % p) - 1; // 进程的最后一个数的索引
    low_value = 2 + low_index; //进程的第一个数
    high_value = 2 + high_index;//进程的最后一个数
    size = high_value - low_value + 1;    //进程处理的数组大小


    // Bail out if all the primes used for sieving are not all held by process 0
    proc0_size = (n - 1) / p;

    // 如果有太多进程
    if ((2 + proc0_size) < (int) sqrt((double) n)) {
        if (!id) printf("Too many processes \n");
        MPI_Finalize();
        exit(1);
    }

    // allocate this process 's share of the array
    marked = (char *) malloc(size);
    if (marked == nullptr) {
        printf("Cannot allocate enough memory \n");
        MPI_Finalize();
        exit(1);
    }

    // 先假定所有的整数都是素数
    for (int i = 0; i < size; i++) marked[i] = 0;

    // 索引初始化为0
    if (!id) index = 0;

    // 从2开始搜寻
    prime = 2;
    do {
        /*确定该进程中素数的第一个倍数的下标 */
        // 如果该素数n*n>low_value，n*(n-i)都被标记了
        // 即n*n为该进程中的第一个素数
        // 其下标为n*n-low_value
        if (prime * prime > low_value) {
            first = prime * prime - low_value;
        } else {
            // 若最小值low_value为该素数的倍数
            // 则第一个倍数为low_value，即其下标为0
            if (!(low_value % prime)) first = 0;
                // 若最小值low_value不是该素数的倍数
                // 那么第一个倍数的下标为该素数减去余数的值
            else first = prime - (low_value % prime);
        }

        // 从第一个素数开始，标记该素数的倍数为非素数
        for (int i = first; i < size; i += prime) marked[i] = 1;

        // 只有id=0的进程才调用，用于找到下一素数的位置
        if (!id) {
            while (marked[++index]); // 先自加再执行
            prime = index + 2; // 起始加偏移
        }

        // 只有id=0的进程才调用，用于将下一个素数广播出去
        if (p > 1) {
            MPI_Bcast(&prime, 1, MPI_INT, 0, MPI_COMM_WORLD);
        }

    } while (prime * prime <= n);

    // 将标记结果发给0号进程
    count = 0;
    for (int i = 0; i < size; i++)
        if (marked[i] == 0) {
            count++;
        }
    MPI_Reduce(&count, &global_count, 1, MPI_INT, MPI_SUM, 0, MPI_COMM_WORLD);

    // stop the timer
    elapsed_time += MPI_Wtime();

    // print the results
    if (!id) {
        printf("%d primes are less than or equal to %d \n", global_count, n);
        printf("Total elapsed time: %10.6f\n", elapsed_time);
    }
    MPI_Finalize();

    if (!id){
        // 以追加的方式打开文件
//        char str1[30] = "../output/record.init.";
//        char str2[10] = ".txt";
//        char filename[50];
//        sprintf(filename, "%s%d%s", str1, p, str2);
//        FILE *fp;
//        if ((fp = fopen(filename,"a+")) == nullptr){
//            printf("fail to open file");
//            exit(0);
//        }
//        fprintf(fp, "%d %d %10.6f\n", p, n, elapsed_time);
//        fclose(fp);
    }
    return 0;
}

优化一：去掉偶数

利用已知除2以外的所有偶数都不是素数的常识，可以将待筛选数字总量减半，从而提高筛选效率。

关键代码在于数组减半，找到新的索引映射，以及首个倍数（非素数）的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int N = (n - 1) / 2;
low_index = id * (N / p) + MIN(id, N % p); // 进程的第一个数的索引
high_index = (id + 1) * (N / p) + MIN(id + 1, N % p) - 1; // 进程的最后一个数的索引
low_value = low_index * 2 + 3; //进程的第一个数
high_value = (high_index + 1) * 2 + 1;//进程的最后一个数
size = (high_value - low_value) / 2 + 1;    //进程处理的数组大小
   
do {
   /*确定该进程中素数的第一个倍数的下标 */
   // 如果该素数n*n>low_value，n*(n-i)都被标记了
   // 即n*n为该进程中的第一个素数
   // 其下标为n*n-low_value，并且由于数组大小减半所以除以2
   if (prime * prime > low_value) {
   	   first = (prime * prime - low_value) / 2;
   } else {
       // 若最小值low_value为该素数的倍数
       // 则第一个倍数为low_value，即其下标为0
       if (!(low_value % prime)) first = 0;
       // 若最小值low_value不是该素数的倍数
       // 但是其余数为偶数，那么第一个非素数的索引为该素数剪去求余除以2
       else if (low_value % prime % 2 == 0) first = prime - ((low_value % prime) / 2);
       // 若最小值low_value不是该素数的倍数
       // 那么第一个倍数的下标为该素数减去余数的值，并且由于数组大小减半所以除以2
       else first = (prime - (low_value % prime)) / 2;
   }
    // 从第一个素数开始，标记该素数的倍数为非素数
    for (int i = first; i < size; i += prime) marked[i] = 1;

    // 只有id=0的进程才调用，用于找到下一素数的位置
    if (!id) {
        while (marked[++index]);
        prime = index * 2 + 3; // 起始加偏移
    }
    // 只有id=0的进程才调用，用于将下一个素数广播出去
    if (p > 1) {
        MPI_Bcast(&prime, 1, MPI_INT, 0, MPI_COMM_WORLD);
    }
} while (prime * prime <= n);

  1. 当prime = 3，考虑序列 15 17 19 21 23，则满足low_value % prime == 0，所以索引 0 即第一个数 15 就是 prime的倍数，这个很好理解

  2. 当prime = 3，考虑序列 3 5 7 9 11 13，则满足prime * prime > low_value，那么first = (prime * prime - low_value) / 2 即第一个非素数索引为 3 即值为 9，这个和前面的一样，主要是减去一个偏移，不难理解

    比较难以理解的是后面两个判断

  3. 当prime = 3，考虑序列 17 19 21 23 25，则满足prime * prime <= low_value，并且满足low_value % prime % 2 == 0，那么first = prime - ((low_value % prime) / 2)，即第一个非素数的位置为 0，即值为·15

  4. 当prime = 3，考虑序列 11 13 15 17 19，则满足prime * prime <= low_value，并且满足low_value % prime % 2 != 0，那么 first = (prime - (low_value % prime)) / 2，即第一个非素数索引为 2，即值为15

我理解了很久，我认为主要是由于每次遇到 prime 与 2 的公倍数的时候性质会发生改变，当prime = 3，考虑原有序列7 8 9 10 11 12 13 14 15 16 17，其中 12 为 2 和 3 的公倍数，排除除 12 以外的其他偶数，该序列为 7 9 11 12 13 15 17，再排除 3 的倍数，该序列为 7 11 12 13 17，问题的本质在于小于等于该数（7,11,13,17）最近的并且为 prime （3）和 2 的公倍数 A 是否为偶数。

对于 11，17而言，即满足条件 3，A为 9，15为奇数，偏差bias（求余）为2，所以可以更进一步判断bias是否为偶数，由于其下一个 prime 倍数的位置只能取[0, prime - 1]，故而 prime 下一个倍数所在的位置为 prime - bias / 2；

对于 7，13 而言，即满足条件 4，A 为 6，12为偶数，偏差bias（求余）为1，同样由于其下一个 prime 倍数的位置只能取[0, prime - 1]，故而 prime 下一个倍数所在的位置为 (prime - bias) / 2。

所有代码见这里

优化二：去掉广播通信

原理：初始的代码是通过进程0广播下一个筛选倍数的素数。进程之间需要通过MPI_Bcast函数进行通信。通信就一定会有开销，特别是在分布式计算机架构上，因此我们让每个进程都各自找出它们的前sqrt(n)个数中的素数，在通过这些素数筛选剩下的素数，这样一来进程之间就不需要每个循环广播素数了，性能得到提高。

核心代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/* 小数组 */
char *sub_marked;       /* sub_mark array */
int sub_low_index;      /* Lowest index on sub_array */
int sub_low_value;      /* Lowest array on sub_array */
int sub_high_index;     /* Highest index on sub_array */
int sub_high_value;     /* Highest index on sub_array */

int sub_n = (int) sqrt((double) n);
int sub_N = (sub_n - 1) / 2;

sub_low_index = 0 * (sub_N / p) + MIN(0, sub_N % p); // 进程的第一个数的索引
sub_high_index = 1 * (sub_N / p) + MIN(1, sub_N % p) - 1; // 进程的最后一个数的索引
sub_low_value = sub_low_index * 2 + 3; //进程的第一个数
sub_high_value = (sub_high_index + 1) * 2 + 1;//进程的最后一个数

sub_marked = (char *) malloc(sub_n);
if (sub_marked == nullptr) {
    printf("Cannot allocate enough memory \n");
    MPI_Finalize();
    exit(1);
}

// 先假定所有的整数都是素数
for (int i = 0; i < sub_n; i++) sub_marked[i] = 0;

// 索引初始化为0
index = 0;

prime = 3;
do {
    // 从小数组开始标只会命中第一个条件
    first = (prime * prime - sub_low_value) / 2;
    // 从第一个素数开始，标记该素数的倍数为非素数
    for (int i = first; i < sub_n; i += prime) {
    	sub_marked[i] = 1;
	}
    while (sub_marked[++index]);
    prime = index * 2 + 3; // 起始加偏移
} while (prime * prime <= sub_n);


/* 大数组 */
do {
    
	...
    while (sub_marked[++index]);
    ...
        
    // if (p > 1) {
    //     MPI_Bcast(&prime, 1, MPI_INT, 0, MPI_COMM_WORLD);
    // }
} while (prime * prime <= n);

此优化所有代码见此

优化三：分块筛选，提高cache命中率

在做这个之前我参考了这篇文章，以及这篇文章介绍的原版论文，对于第三个有两个优化思路，第一个是基于cache_linesize的优化，另外一个是基于cache_size的优化，现在来介绍一下如何获取cache的相关信息吧。

linux

在命令行中输入

1
getconf -a | grep CACHE

10

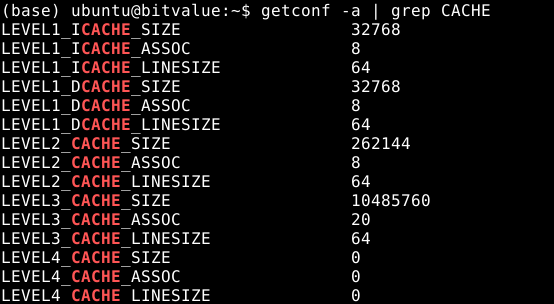
可以看到不同级别的cache的相关信息，包括cache的大小size，cache每行的大小linesize，cache的链接形式n路组相连。

windows

在任务管理栏的性能中

11

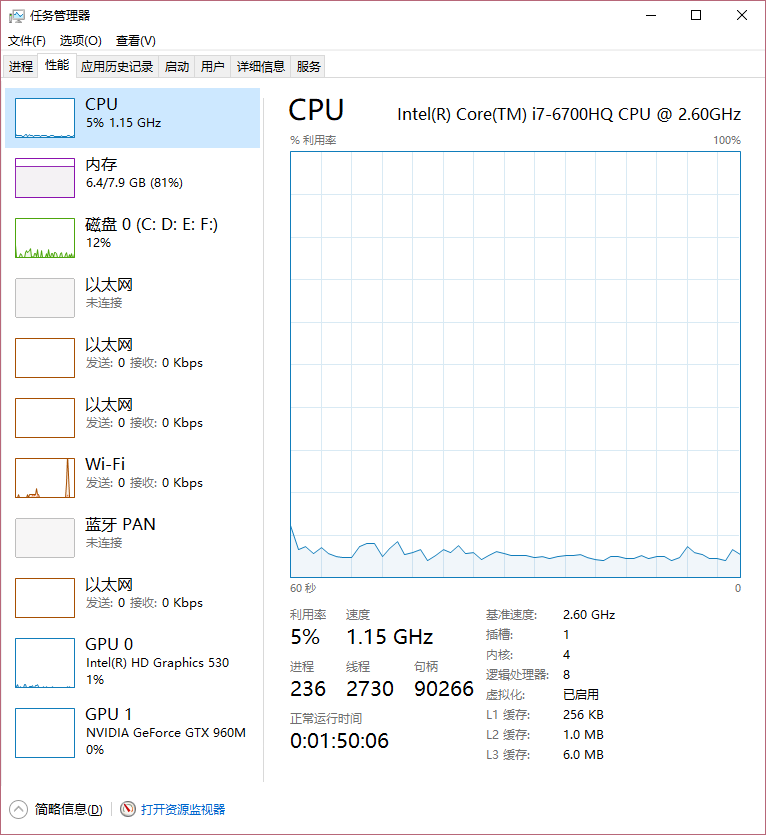
优化

对于大规模的数组来说cache_line的优化效果并不是很明显，所以下面只针对cache做优化，本优化方法需每个进程都各计算出前sqrt(n)个数中的素数，(对应优化思路2)。由于从cache读取的速度远高于从内存中处理，所以cache_size优化的思路在于每次处理cache大小的数组，之前我们已经将n内分成大小约为n/p的块给每个进程处理，然后在在每个进程中将n/p大小块按照cache_size进行分块，在此之前我们需要对cache的大小从byte转化为int，32位系统即除以4，以上图windows为例，L1，L2，L3缓存分别可以存64KB，0.25MB，1.5MB个int，而单机（注意是单机，如果是分布式计算机理论上可以占满所有的cache）中每个进程又将划分其中的cache，如果对于L3而言如果分配 2 个进程则每个进程能够得到 0.75 MB个int进程处理，而实际中由于计算机中有其他进程也会使用cache，所以在实际中这个数还要小。另外根据测试的时候n大小进行选择cache的级别，比如我测试的是亿级的数据，远超过cache的大小，所以直接对L3级别的cache进行分块，当然选择L3并不一定是最优策略，需要多次实证才能知道。

故基于此关键代码在于进程内分块：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
int LEVEL1_CACHE_size = 32768;      // default 32768
int LEVEL2_CACHE_size = 262144;     // default 262144
int LEVEL3_CACHE_size = 9485760;    // default 10485760

int LEVEL1_CACHE_int = LEVEL1_CACHE_size / 4;
int LEVEL2_CACHE_int = LEVEL2_CACHE_size / 4;
int LEVEL3_CACHE_int = LEVEL3_CACHE_size / 4;

int Block_size = LEVEL3_CACHE_int / p ;
int Block_num = size / Block_size;
int Block_remain = size % Block_size;

int Block_id = 0;
int Block_N = Block_size - 1;
int Block_low_index = Block_id * Block_N + MIN(Block_id, Block_remain) + low_index;
int Block_high_index = (Block_id + 1) * Block_N + MIN(Block_id + 1, Block_remain) - 1 + low_index;
int Block_low_value = Block_low_index * 2 + 3;
int Block_high_value = (Block_high_index + 1) * 2 + 1;
int Block_count;

// allocate this process 's share of the array
marked = (char *) malloc(Block_size);
if (marked == nullptr) {
    printf("Cannot allocate enough memory \n");
    MPI_Finalize();
    exit(1);
}

// 总计数
count = 0;

while (Block_id <= Block_num) {

    // 索引初始化为0
    index = 0;

    // 从3开始搜寻，first为第一个不是素数的位置
    prime = 3;

    // 块计数
    Block_count = 0;

    // 先假定块中的整数都是素数
    for (int i = 0; i < Block_size; i++) marked[i] = 0;

    // 在块内找素数
    do {
        /*确定该进程中素数的第一个倍数的下标 */
        // 如果该素数n*n>low_value，n*(n-i)都被标记了
        // 即n*n为该进程中的第一个素数
        // 其下标为n*n-low_value，并且由于数组大小减半所以除以2
        if (prime * prime > Block_low_value) {
            first = (prime * prime - Block_low_value) / 2;
        } else {
            // 若最小值low_value为该素数的倍数
            // 则第一个倍数为low_value，即其下标为0
            if (!(Block_low_value % prime)) first = 0;
                // 若最小值low_value不是该素数的倍数
                // 但是其余数为偶数，那么第一个非素数的索引为该素数剪去求余除以2
            else if (Block_low_value % prime % 2 == 0) first = prime - ((Block_low_value % prime) / 2);
                // 若最小值low_value不是该素数的倍数
                // 那么第一个倍数的下标为该素数减去余数的值，并且由于数组大小减半所以除以2
            else first = (prime - (Block_low_value % prime)) / 2;
        }

        // 从第一个素数开始，标记该素数的倍数为非素数
        for (int i = first; i < Block_size; i += prime) {
            marked[i] = 1;
        }

        // 用于找到下一素数的位置
        while (sub_marked[++index]);

        prime = index * 2 + 3; // 起始加偏移

    } while (prime * prime <= Block_high_value);

    // 统计块内计数
    for (int i = 0; i < Block_size; i++) {
        if (marked[i] == 0) {
            Block_count++;
        }
    }

    // 汇总总体计数
    count += Block_count;


    // 处理下一个块
    Block_id++;
    Block_low_index = Block_id * Block_N + MIN(Block_id, Block_remain) + low_index;
    Block_high_index = (Block_id + 1) * Block_N + MIN(Block_id + 1, Block_remain) - 1 + low_index;
    Block_low_value = Block_low_index * 2 + 3;
    if (Block_id == Block_num) {
        Block_high_value = high_value;
        Block_high_index = high_index;
        Block_size = (Block_high_value - Block_low_value) / 2 + 1;
    } else {
        Block_high_value = (Block_high_index + 1) * 2 + 1;
    }

}

此优化所有代码见此

项目

地址

项目地址为https://github.com/543877815/uestc_Internet_plus_course_project/tree/master/parallel_programming

目录说明

linux

本项目原本是在linux环境下使用clion基于mpich进行开发，相关目录及文件说明如下：

  • main.cpp为原版代码
  • main1.cpp为去掉偶数优化代码
  • main2.cpp为去掉通信代码
  • main3.cpp为初步提升cache命中率代码
  • MPItest.cpp为起初测试linux下mpi环境代码
  • base.cpp为原版代码副本
  • cache.test.cpp为阅读本文的测试代码
  • output为输出结果（输出已在代码中注释需要手动取消）。

windows

后来在windows上进行测试，使用VS对代码进行部分修改以兼容windows版本并进行了编译，其中

  • srcForWindows为存放了windows下运行源码目录

  • execForWindows为编译生成的可执行文件

    • 需要安装msmpisetup.exe
    • 执行命令为mpiexec -n 8 main.exe 10000000
    • main3.exe需要传入cache_size的参数 mpiexec -n 8 main.exe 10000000 10240000
    • 生成数据文件需要手动在该目录下创建名为output的文件夹

  • 你可能需要的文件

优化效果及加速比

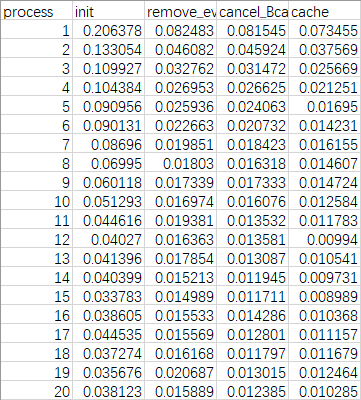
我跑的是找1亿以内的素数，结果为5761455个，在我的电脑上运行时间如下图

12

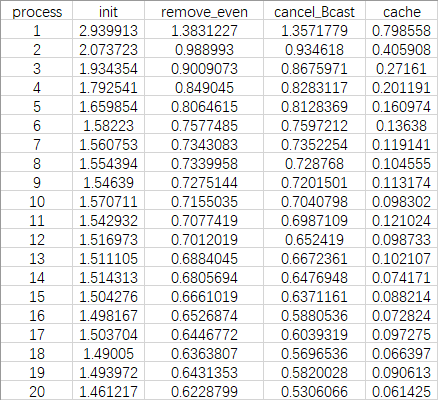
  • 横向对比可以看出通过优化一去掉偶数可以使待处理数组减半，故而时间减半；通过优化二去掉通信在单机上进程数量较少的时候优化效果不明显，随着进程数量增加，优化效果有所提升，如果考虑分布式计算机，优化效果会更加明显；通过优化三增加cache命中率可以显著提升优化效果。

  • 而纵向对比可以发现随着处理器的增加使得运行时间有所减少。

加速比

加速比的定义为

其中：

  • $p$指CPU数量
  • $T_1$指顺序执行算法的执行时间
  • $T_p$指当有p个处理器时，并行算法的执行时间

规模为1,0000,0000的时候绘制的加速比 – 处理器曲线如下

可以发现通过优化一去除偶数使得运行时间减半，加速比表现为原始版本的两倍，而通过优化二去掉通信在单机上优化效果不太明显，但在进程较多的时候还是有所体现，因此，加速比比优化一还是有所提升。当Sp=p时，Sp便可以称为“线性加速比”，即当某一并行算法的加速比为理想加速比时，若将处理器数量加倍，执行速度也会加倍，但是在规模1,0000,0000的情况下除cache优化外其他三种代码并没有表现出这种趋势，初步分析认为这是由于i/o而不是计算占程序的主要部分导致的。

因此为了让计算占据更多程序运行的更大部分，我将规模增加为10,0000,0000后再进行对比：

13

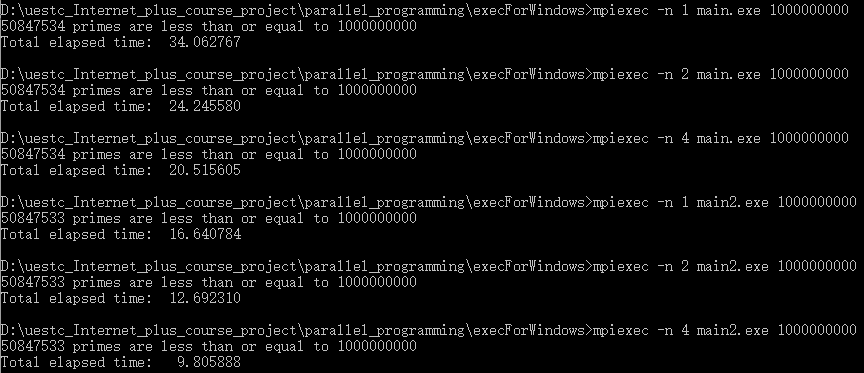
可以发现情况依然如此，因此我姑且得出的结论是前三种代码并不是能够产生理想加速比的代码，当然这存在的着通信开销以及一些其他的系统运行开销的影响。

而通过cache缓冲后加速比，在前8核加速比按照处理器核数线性增加，达到8核以后有加速比有上升的趋势但是也有所波动并且不再呈现线性的趋势，因为处理器有限不能同时处理多个任务，这与之前查看windows系统CPU配置的4核8处理器相符。另外有Sp>p，即产生了超线性加速比，通过维基百科得知，超线性加速比有几种可能的成因，如现代计算机的存储层次不同所带来的“高速缓存效应”；具体来说，较之顺序计算，在并行计算中，不仅参与计算的处理器数量更多，不同处理器的高速缓存也集合使用。而有鉴于此，集合的缓存便足以提供计算所需的存储量，算法执行时便不必使用速度较慢的内存，因而存储器读些时间便能大幅降低，这便对实际计算产生了额外的加速效果。

并行效率

由加速比派生出的效率（英语：efficiency）则是量度性能的指标，并如下定义：

绘制的并行效率与执行进程数的曲线如下：

可以看到没有使用cache优化的时候并行效率一般介于0~1之间，通过cache命中优化使得产生超线性加速比并且并行效率大于1。

其他规模

规模为10,000,000，则素数有664579个，运行时间如下

14

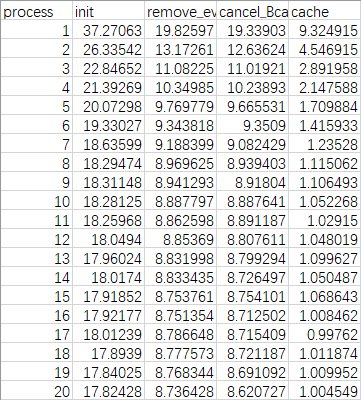
规模为10,0000,0000，则素数有50847533个，运行时间如下

15