Ensemble Learning

Adaboost、GBDT、xgboost的个人理解

前向分布算法

Adaboost

基本步骤

Adaboost 算法的基本原理就是将多个弱分类器进行结合，最终成为一个强分类器。与 bagging 不同的是，这个弱分类器的训练不是并行化的，而是采用一种迭代的方式。其基本步骤就是：

• 每次训练只训练一个弱分类器，训练好的弱分类器将参与到下一次迭代，也就是说第 N 次迭代中会有 N-1 个分类器是之前就训练好的，在其他参数不变的情况下训练第 N 个分类器。
• 该第 N 个分类器训练的时候，要找到一组新的训练数据，让前面 N-1 个分类器在其上的表现很差，然后让第 N 个分类器这组数据上训练。怎么找到这组新的训练数据，其实就是权重的调整，其思想就是第 N 个分类器将着重关注前面 N-1 个分类器中分错的样本，即通过重采样的方法给予这些数据更高的权重，也相当于改变样本的概率分布，这将使得前 N-1 个分类器在该样本上表现不佳，而只要第 N 个分类器在该样本上正确分类即能获得很高的性能。
• 最终，在此基础上，对所有 N 个弱分类器采用加权投票的方法来对测试样本进行预测，这 N 个弱分类器的权重将由其分类正确率来决定，正确率越高的弱分类器在强分类器中拥有更大的权重。

具体流程

自己总结的计算具体流程：

• 假设有$N$个训练样本$\{(x_1,y_1),...(x_N,y_N)\},y_i\in\{-1,+1\}$，第 1 次迭代每个样本的权重初始化为：

  $$w_{1i}=\frac{1}{N},i=1,2,...N$$

• 第 k 次迭代中的分类器 $C$ 的样本加权错误率为（分母为权重归一化）：

$$\epsilon_k=\frac{\sum_{i=1}^Nw_{ki}C(f_k(x_i)\ne(\hat y_i))}{\sum_{i=1}^Nw_{ki}}$$

• 对于错误分类的样本，其第 k+1 次迭代的权重将被调整为：

  $$w_{(k+1)i}=w_{ki}*d_k$$

  对于正确分类的样本，其第 k+1 次迭代的权重将被调整为：

  $$w_{(k+1)}i=\frac{w_{ki}}{d_k}$$

  其中$d_k=\sqrt\frac{1-\epsilon_k}{\epsilon_k}$，由于错误率（二分类问题）是一个小于 0.5 的数，所以$d_k$是一个大于 1 的数，权重调整目的是使错误样本的权重更高，在下一轮迭代中有更高的概率被选中，降低正确样本的选中概率。

• 为了统一描述权重的更新往往用$a_k=\frac{1}{2}ln(\sqrt\frac{1-\epsilon_k}{\epsilon_k})$来替代$d_k$，这样权重的更新可以描述为：

  $$w_{(k+1)i}=w_{ki}*\exp{(-\hat y^if_k(x^i)a_t)}$$

  同时权重更新完之后需要对权重进行归一化使得$\sum_{i=1}^N w_ki=1$（其实就是上面第二步分母做的事情，主要是保证加权误差率的正确）。

• 另外，新训练好的弱分类器将加入到集成模型中：

  $$F_k(x)=F_{k-1}(x)+a_kf_k(x)$$

• 最后，强分类器将表达为 $k$ 次迭代的 $k$ 个弱分类器的权重和：

  $$F_k(x)=sign(\sum_{i=i}^ka_if_i(x))$$

运算案例

下面是一个李宏毅老师深度学习的例子以帮助理解：

• 

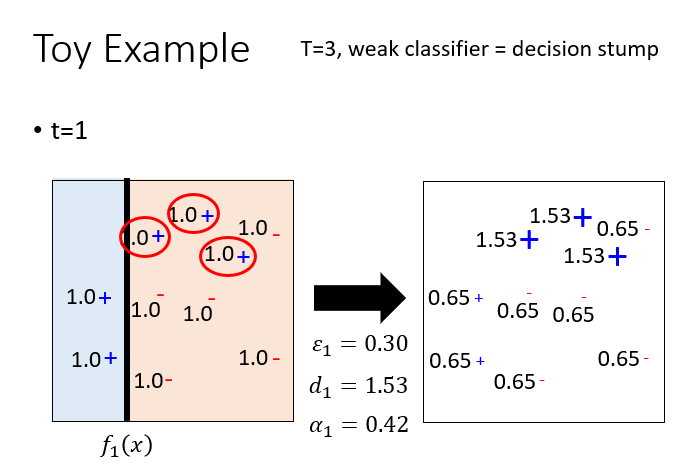
初始一共有10个样本，并且每个样本的权重是一致的，假如有这么一个弱分类器$f_1(x)$，其产生的决策边界如图黑线所示，其中蓝色区域为其分类的正样本，红色区域为其分类的负样本，那么一共有三个被红色圈中的样本分类错误，所以第一次迭代的错误率$\epsilon_1=0.30$，那么$d_1=\sqrt\frac{1-\epsilon_1}{\epsilon_1}=\sqrt\frac{1-0.3}{0.3}\approx1.53$，那么分类正确的样本权重将调整为$w_{2i}=\frac{w_{1i}}{d_1}=0.65$，分类错误的样本权重将调整为$w_{2i}=w_{1i}*d_i=1.53$，第 1 个弱分类器的权重$a_1=ln(d_1)=0.42$，这个例子讲的时候$a_k$没有乘$\frac{1}{2}$。

• 

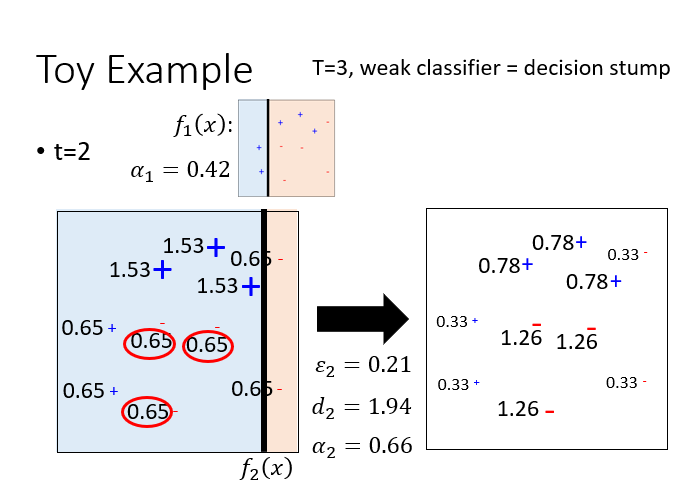
这是第 2 次迭代。

• 

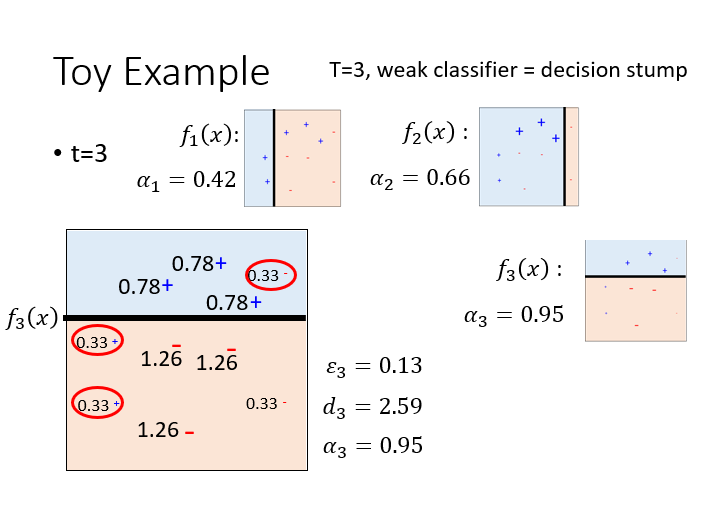
这是第 3 次迭代。

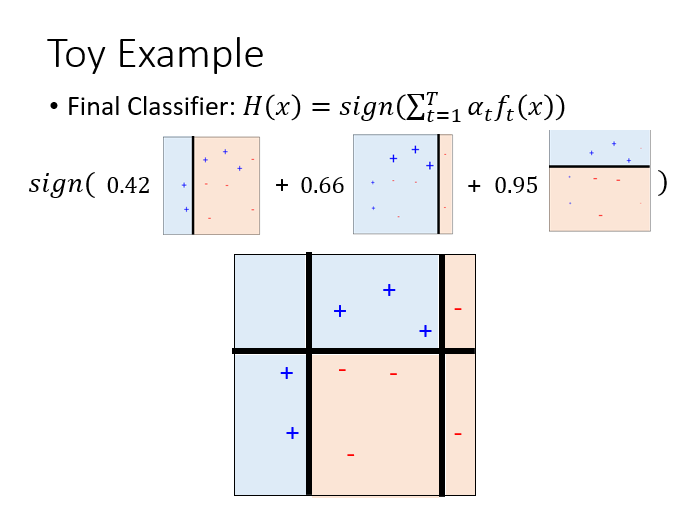
最终所有弱分类器的加权组合将会得到一个强分类器，这个强分类器将会正确分类这个实例的所有样本。

看了很多例子，这个例子对我来说最形象生动，但是注意这个例子的权重调整没有进行归一化。

公式推导

证明：为什么$a_k=\frac{1}{2}ln(\sqrt\frac{1-\epsilon_k}{\epsilon_k})$？

• 假如有一个训练集$\{(x_1,y_1), (x_2,y_2),...,(x_N,y_N)\}, y_i\in\{-1,1\}$，在第 m-1 次迭代后已经有一个多种弱分类器组合而成的线性分类器：

  $$C_{(m-1)}(x_i)=a_1k_1(x_i)+...+a_{(m-1)}k_{(k-1)}(x_i)$$

• 在第 m 次迭代将要训练第 m 个弱分类器$k_m$，它的权重是$a_m$，使之成为一个更强的分类器：

  $$C_m(x_i)=C_{(m-1)}(x_i)+a_mk_m(x_i)$$

• 所以仍然需要确定弱分类器$k_m$及其权重$a_m$，因此定义强分类器$C_m$总指数误差为：

  $$E=\sum_{i=1}^Ne^{-y_iC_m(c_i)}=\sum_{i=1}^Ne^{-y_iC_{m-1}(x_i)}e^{-y_ia_mk_m(x_i)}$$

  注：指数误差通常用在boosting中，指数误差始终大于 0，但是确保越接近正确的结果误差越小，反之越大。

• 令 $w_i^{(1)}=1$ 以及 $w_i^{(m)}=e^{-y_iC_{m-1}(x_i)},m>1$，可以将上式简化为

  $$E=\sum_{i=1}^Nw_i^{(m)}e^{-y_ia_mk_m(x_i)}$$

• 我们可以将上式写成下面这种形式（即将错误分类和正确分类的误差进行求和）：

  $$E=\sum_{y_i=k_m(x_i)}w_i^{(m)}e^{-a_m}+\sum_{y_i\ne k_m(x_i)}w_i^{(m)}e^{a_m}$$

  这意味着总误差是所有正确分类和错误分类的加权误差和。

• 由于$w_i$是一个常数，为了找到一个新的弱分类器权重$a_m$能够最小化误差$E$，则对$E$进行求导：

  $$\frac{dE}{da_m}=\frac{d(\sum_{y=k_m(x_i)}w_i^{(m)}e^{-a_m}+\sum_{y\ne k_m(x_i)}w_i^{(m)}e^{a_m})}{da_m}$$

• 令上述公式为 0 可以求得

  $$\begin{align}&\frac{dE}{da_m}=-\sum_{y_i=k_m(x_i)}w_i^{(m)}e^{-a_m}+\sum_{y_i\ne k_m(x_i)}w_i^{(m)}e^{-a_m}=0\\\text{because }&e^{-a_m}\text{ does not depend on }i\\&\sum_{y_i=k_m(x_i)}w_i^{(m)}e^{-a_m} = \sum_{y_i\ne k_m(x_i)}w_i^{(m)}e^{-a_m}\\&-a_m+log(\sum_{y_i=k_m(x_i)}w_i^{(m)})=a_m+log(\sum_{y_i\ne k_m(x_i)}x_i^{(m)})\\&-2a_m=log(\frac{\sum_{y_i\ne k_m(x_i)}w_i^{(m)}}{\sum_{y_i=k_m(x_i)}w_i^{(m)}})\\&a_m=-\frac{1}{2}log(\frac{\sum_{y_i\ne k_m(x_i)}w_i^{(m)}}{\sum_{y_i=k_m(x_i)}w_i^{(m)}})\\&a_m=\frac{1}{2}log(\frac{\sum_{y_i=k_m(x_i)}w_i^{(m)}}{\sum_{y_i\ne k_m(x_i)}w_i^{(m)}})\\\end{align}$$
  $$a_m=\frac{1}{2}ln(\frac{\sum_{y_i=k_m(x_i)}w_i^{(m)}}{\sum_{y_i\ne k_m(x_i)}w_i^{(m)}})=\frac{1}{2}ln(\frac{1-\epsilon_m}{\epsilon_m})$$

  其中$\epsilon_m=\frac{\sum_{y_i\ne k_m(x_i)}w_i^{(m)}}{\sum_{i=1}^Nw_i^{(m)}}$。

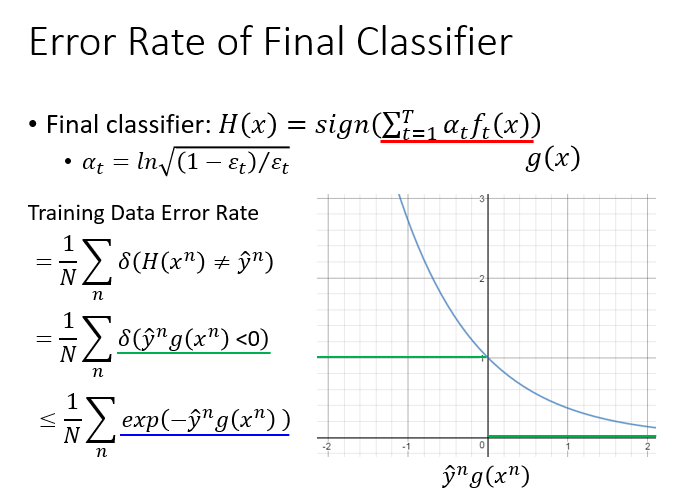
证明：Adaboost随着迭代次数增加，误差率会越来越小。

结合上图，误差函数将被定义为

$$\delta(x)= \begin{cases} 0,\hat y^ng(x^n) > 0\\ 1,\hat y^ng(x^n) < 0\\ \end{cases}\\ 其中，g(x)=\sum^{T}_{t=1}a_tf_t(x)$$

从图中可直观的感受到其小于等于一个上界函数$\sum_n e^{-\hat y^ng(x^n)}$。这个式子实际上等于第 T 次迭代的样本权重和$Z_{T+1}=\sum_n w_n^{(T+1)}$。证明如下：

根据

$$\begin{align} \begin{cases} &w_n^{(1)}=1 \\ &w^{(t+1)}_n=w_t^n*e^{-\hat y^nf_t(x^n)a_t} \end{cases} \Rightarrow w^{(T+1)}_n=\prod_{t=1}^{T}e^{-\hat y^nf_t(x^n)a_t} \end{align}$$

则

$$\begin{align} Z_{T+1}&=\sum_nw_n^{(T+1)}\\ &=\sum_n\prod_{t=1}^{T}e^{-\hat y^nf_t(x^n)a_t}\\ &=\sum_ne^{-\hat y^n\sum_{t=1}^Tf_t(x^n)a_t}\\ &=\sum_ne^{-\hat y^ng(x^n)}\\ \end{align}$$

下面要证明该上界函数将越来越小:

根据

$$\begin{align} Z_1&=N\\ Z_t&=Z_{t-1}\epsilon_te^{a_t}+Z_{t-1}(1-\epsilon_t)e^{-a_t} \\ &\text{ (上式左部表示错误分类的样本，右部表示正确分类的样本)}\\ &=Z_{t-1}\epsilon_t\sqrt\frac{1-\epsilon_t}{\epsilon_t}+Z_{t-1}(1-\epsilon_t)\sqrt\frac{\epsilon_t}{1-\epsilon_t}\\ &=Z_{t-1}*2\sqrt {\epsilon_t(1-\epsilon_t)} \end{align}$$

如果使用递推的方式则有

$$Z_{T+1}=N\prod_{t=1}^T2\sqrt{\epsilon_t(1-\epsilon_t)}$$

结合上述证明，结论是：

$$\delta(x)\le\prod_{t=1}^T2\sqrt{\epsilon_t(1-\epsilon_t)}$$

由于$\epsilon_t<0.5$，所以训练数据的错误率会随着迭代次数的增加而越来越小。

令 $\gamma_m=\frac{1}{2}-\epsilon_t$，则 $\gamma\gt0$，有

$$\prod_{t=1}^T2\sqrt{\epsilon_t(1-\epsilon_t)}=\prod_{t=1}^T\sqrt{1-4\gamma_m^2}\le e^{-2\sum_{t=1}^T\gamma_m^2}$$

证明如下（自文哥的学习日记）：

要证：

$$\prod_{t=1}^T\sqrt{1-4\gamma_m^2}\le e^{-2\sum_{t=1}^T\gamma_m^2}$$

即证：

$$\sqrt{1-4\gamma^2_m}\le e^{-2\gamma^2_m} \\ 1-4\gamma_m^2\le e^{-4\gamma_m^2} \\$$

令 $x=4\gamma_m^2$，因为$\gamma_m=\frac{1}{2}-e_m,e_m\in[0,1]$，所以 $\gamma_m\in[-\frac{1}{2},\frac{1}{2}]$，所以 $x\in[0,1]$，令：

$$f(x)=e^{-x}+x-1$$

则：

$$f'(x)=-e^{-x}+1\ge0$$

所以 $f(x)$ 递增，又因为 $f(0)=0$，所以 $f(x)\ge 0$ 在 $x\in[0,1]$ 上成立，故原式得证。

推论：如果存在 $\gamma\gt0$，对所有 $m$ 有$\gamma_m\ge\gamma$，则

$$\frac{1}{T}\sum_{i=1}^TI(G(x_i)\ne y_i)\le e^{-2T\gamma^2}$$

参考

paper: AdaBoost and the Super Bowl of Classifiers A Tutorial Introduction to Adaptive Boosting

李宏毅深度学习：https://datawhalechina.github.io/leeml-notes/#/chapter38/chapter38?id=adaboost

wikipedia.org: https://en.wikipedia.org/wiki/AdaBoost

李航：统计学习方法第二版

网站：https://www.jianshu.com/u/c5df9e229a67

实现：参考@ljpzzz

GBDT

使用前向分布算法构建提升树：

$$\begin{align} &f_0(x)=0\\ &f_m(x)=f_{m-1}(x)+T(x;\Theta_m),\;\;m=1,2,...,M\\ &f_M(x)=\sum_{m=1}^MT(x;\Theta_m) \end{align}$$

需要求解最小化损失函数的参数$\Theta$：

$$\hat\Theta=\arg\;\min_{\Theta_m}\sum_{i=1}^NL(y_i,f_{m-1}(x_i)+T(x_i;\Theta_m))$$

当采用平方误差损失函数时：

$$\begin{align} L(y,f(x))&=(y-f(x))^2\\ L(y,f_{m-1}(x)+T(x;\Theta_m))&=[y-f_{m-1}(x)-T(x;\Theta_m)]^2\\ &=[r-T(x;\Theta)]^2 \end{align}$$

这里 $r$ 是当前模型拟合数据的误差 $r=y-f_{m-1}(x)$

算例：

参考

梯度提升树(GBDT)原理小结[

scikit-learn 梯度提升树(GBDT)调参小结

李航：统计学习方法第二版

XGBoost

XGBoost算法原理小结

XGBoost类库使用小结