【论文笔记】 Towards Evaluating the Robustness of Neural Networks

今天读了一下 Towards Evaluating the Robustness of Neural Networks，这是关于对抗样本(Adversarial Example)的paper，主要贡献是提出了Carlini & Wagner Attack神经网络有目标攻击算法，打破了最近提出的神经网络防御性蒸馏(Defensive Distillation)，证明防御性蒸馏不会显著提高神经网络的鲁棒性，论文的信息量还是比较大的。

可能需要阅读的论文以获取前置知识：

关于蒸馏网络：

[1] Do Deep Nets Really Need to be Deep?

[2] Distilling the Knowledge in a Neural Network

[3] Distillation as a Defense to Adversarial Perturbations against Deep Neural Networks

关于对抗样本：

[4] Intriguing properties of neural networks（L-BFGS Attack）

[5] Exploring the Space of Adversarial Images（FGSM）

[6] Towards Deep Learning Models Resistant to Adversarial Attacks（PGD, I-FGSM）

[7] The Limitations of Deep Learning in Adversarial Settings (JSMA)

[8] DeepFool: a simple and accurate method to fool deep neural networks（DeepFool）

关于论文源码：

carlini/nn_robust_attacks

对抗样本 (Adversarial Example)

Basic Idea

通过故意对数据集中输入样例添加难以察觉的摄动使模型以高置信度给出一个错误的输出。即只需要在一张图片上做微小的扰动，(神经网络)分类器以很高的置信度将图片错误分类，甚至被分类成一个指定的标签（不是图片正确所属的标签）。

这类问题可以表述为一个约束最小化问题：

$$\text{minimize}\;\;D(x,x+\delta)\\ \begin{align} \text{such that}\;\ & C(x+\delta)=t\\ &x+\delta\in[0,1]^m \end{align}$$

其中：

• $x\in R^m$ 是干净图片向量。
• $\delta \in R^m$ 是被加入到图片的扰动。
• $D(.)$ 是距离度量。
• $t$ 是攻击的目标标签。
• $C(.)$是深度神经网络分类器。
• $[0,1]^m$ 用于限制扰动后值的范围。

对于距离度量而言，$L_p$ 距离常常被写作$||x-x'||_p$，其 $p$ 范数被定义为：

$$||v||_p=(\sum_{i=1}^n|v_i|^p)^{\frac{1}{p}}$$

具体而言：

• $L_0$ 距离度量的是 $x_i\ne x_i'$ 的坐标 $i$ 的数量，其对应的是图像中被改变的像素的数量。
• $L_2$ 距离度量的是 $x_i$ 和 $x_i'$ 之间的欧式距离，当许多像素发生小变化时，$L_2$ 依据可以保持较小。
• $L_\infty$ 距离度量的是 $x_i$ 和 $x_i'$ 之间最大的绝对距离即$||x-x'||\infty=max(|x_1-x_1'|,...,|x_n-x_n’|)$，每个像素可以被改变到这个极限。

Objective Function

由于该目标函数一个高度非线性的函数，现有算法很难直接求解上述公式，往往通过将其表述为一个适当的优化公式来解决，而这个优化公式可以通过现有的优化算法来解决。论文定义了新的目标函数$f$，使得 $f(x+\delta)\le0$ 当且仅当 $C(x+\delta)=t$ 成立，论文探索了公式的空间，并根据经验确定哪些公式可以导致最有效的攻击，提出了七个目标函数，公式如下（附上个人理解，所有的目标函数似乎都有大于等于0的约束）：

• $f_1(x')=-loss_{F,t}(x')+1$，对目标标签的损失函数进行优化，这个目标函数和 L-BFGS Attack 相类似。
• $f_2(x')=(\max_{i\ne t}(F(x')_i)-F(x')_t)^+$，对目标标签的置信度进行优化，希望其成为最后预测值。
• $f_3(x')=\text{softplus}(\max_{i\ne t}(F(x')_i)-F(x')_t)-log(2)$， 也是对目标标签的置信度进行优化，形式不同。
• $f_4(x')=(0.5-F(x')_t)^+$，也是对目标标签的置信度进行优化，希望其成为最大可能类。
• $f_5(x')=-log(2F(x')_t-2)$，同 $f_4$。
• $f_6(x')=(\max_{i\ne t}(Z(x')_i)-Z(x')_t)^+$，对目标标签的 logit 值进行优化。同 $f_2$.
• $f_7(x')=\text{softplus}(\max_{i\ne t}(Z(x')_i)-Z(x')_t)-log(2)$，也对目标标签的 logit 值进行优化，同 $f_3$.

其中：

$s$ 是正确的分类，$(e)^+$ 是 $\max(e,0)$ 的缩写，$\text{suftplus}(x) = \text{log}(1+\text{exp}(x))$，$loss_{F,s}(x)$是关于$x$的交叉熵损失，$Z||.||$ 是最后一个隐藏层的输出，即 logit 层，$F||.||$ 是经过 softmax 后的输出，如图示：

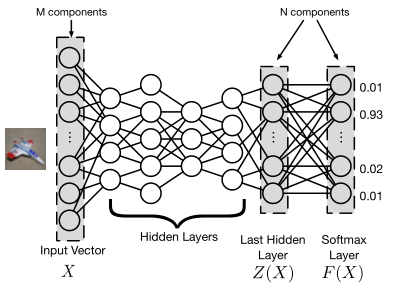
现在把原始问题表述为：

$$\begin{cases} \text{minimize}\;\;&D(x,x+\delta)\\ \text{such that}\; &C(x+\delta)=t\\ &x+\delta\in[0,1]^m \end{cases} \Rightarrow \begin{cases} \text{minimize}\;\;&D(x,x+\delta)+c \,·\,f(x+\delta) \\ \text{such that}\; &x+\delta\in[0,1]^m \\ \end{cases}$$

其中 $c\gt0$ 是一个惩罚因子，用于权衡目标和约束的重要性，有点像正则化，论文通过二分查找法来选择合适的 $c$，下图是 $c$ 的敏感度，可以看出在 $L_2$ 约束和 $f_6$ 目标函数的前提下，当 $c\lt 1$，攻击成功率很低。在 $c \gt 1$ 之后，攻击效果提升不大，但成功率很高。

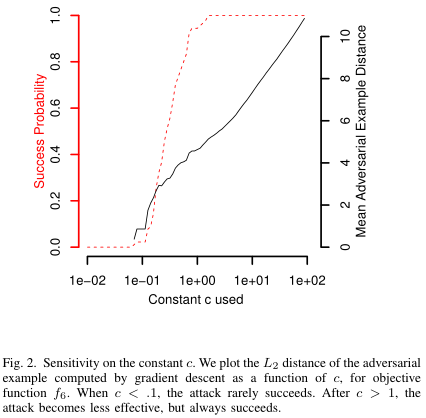
Box constraints

为了确保生成有效的图片，对于像素点的扰动 $\delta$ 存在着约束 $0\le x_i+\delta_i\le1$，在优化问题中，这个被称为“盒约束”。该论文研究了三种不同方法来解决这个问题：

第一个方法是Projected gradient descent，在每次迭代中，执行一个单步标准梯度下降后，将所有坐标约束到 $[0,1]$ 的范围内，这个方法的性能不佳，原因在于它将剪辑后的图片作为下一次迭代的输入。（这个方法的具体表述不是很清楚，需要看看源码）

第二个方法是Clipped gradient descent，上述方法存在一个问题就是算法可能会卡在一个平坦的点上，即当像素增加了一个比允许的最大值大得多的分量的时候，再将其约束到 1，那么偏导数就会变成 0。所以这个方法将盒约束整合到目标函数中，即目标函数从 $f(x+\delta)$ 转化为 $f(\min{(\max{(x+\delta,0)},1)})$。

第三个方式是Change of variables，该方法引入一个新的变量 $\omega$，将上述优化 $\delta$ 的问题转化为优化 $\omega$，通过定义：

$$\delta_i=\frac{1}{2}(tanh(\omega_i)+1)-x_i$$

因为$-1\le tanh(\omega_i) \le1$，所以$0\le x_i+\delta_i\le1$ 是成立的，这样的转化允许我们使用其他不支持盒约束的算法进行优化，论文尝试了三种求解方法：标准梯度下降法、动量梯度下降法以及Adam算法，并且发现这三种算法都得到相同质量的解，然而Adam算法的收敛速度最快。

Evaluation of approach

由于这是有目标攻击：论文考虑了三种不同的策略来选择目标类，分别是：

• Average Case: 在不正确的标签中随机均匀地选择目标类。
• Best Case: 对所有不正确的类执行攻击，并报告最易攻击的目标类。
• Worst Case: 对所有不正确的类执行攻击，并报告最难攻击的目标类。

下图图示为在不同目标类选择策略中，三个不同盒约束中，七个可能目标函数的前提下，$L_2$ 的平均距离、标准偏差(where?)和攻击成功概率。另外，当攻击成功率不是100%时，平均距离仅计算了攻击成功的部分。

从中可以发现看出Projected gradient descent在处理盒约束成功率是优于另外两种策略，而Change of variables往往能找到更小的扰动，对于目标函数而言，$f_6$表现的比其他的好，扰动最小，成功率最高。为什么有些损失函数比其他函数更好？论文认为原因在于当 $c=0$ 的时候，梯度下降法不会改变原始图像，但是如果 $c$ 较大的时候往往会导致梯度下降的初始步骤过于贪婪，只沿着最容易降低 $f$ 的方向移动，而忽略了 $D$ 的损失，从而导致梯度下降找到次优解。论文认为 $f_1$ 和 $f_4$ 的表现相对较差，找不到一个合适的 $c$，因为 $c$ 权衡了距离约束项和损失函数项的重要性，如果要找到一个固定的常数 $c$，那么这两项的值应该保持相对一致。对于 $f_4$，论文做了一个实验就是将 $x$ 和 $x’$ 进行线性组合构造 $y=\alpha x+(1-\alpha) x'\;，\alpha\in[0,1]'$，事实发现从干净样本到对抗样本（$\alpha$ 从 0 到 1）， $Z(.)_t$的值基本是线性的，因此 $F(.)_t$ 应该是一个logistic函数，论文实验验证结果的皮尔斯相关系数 $r\gt 0.9$ 证明$F(.)_t$服从该分布。那么，对于 $f_4(x')=(0.5-F(x')_t)^+$，其图像应该为

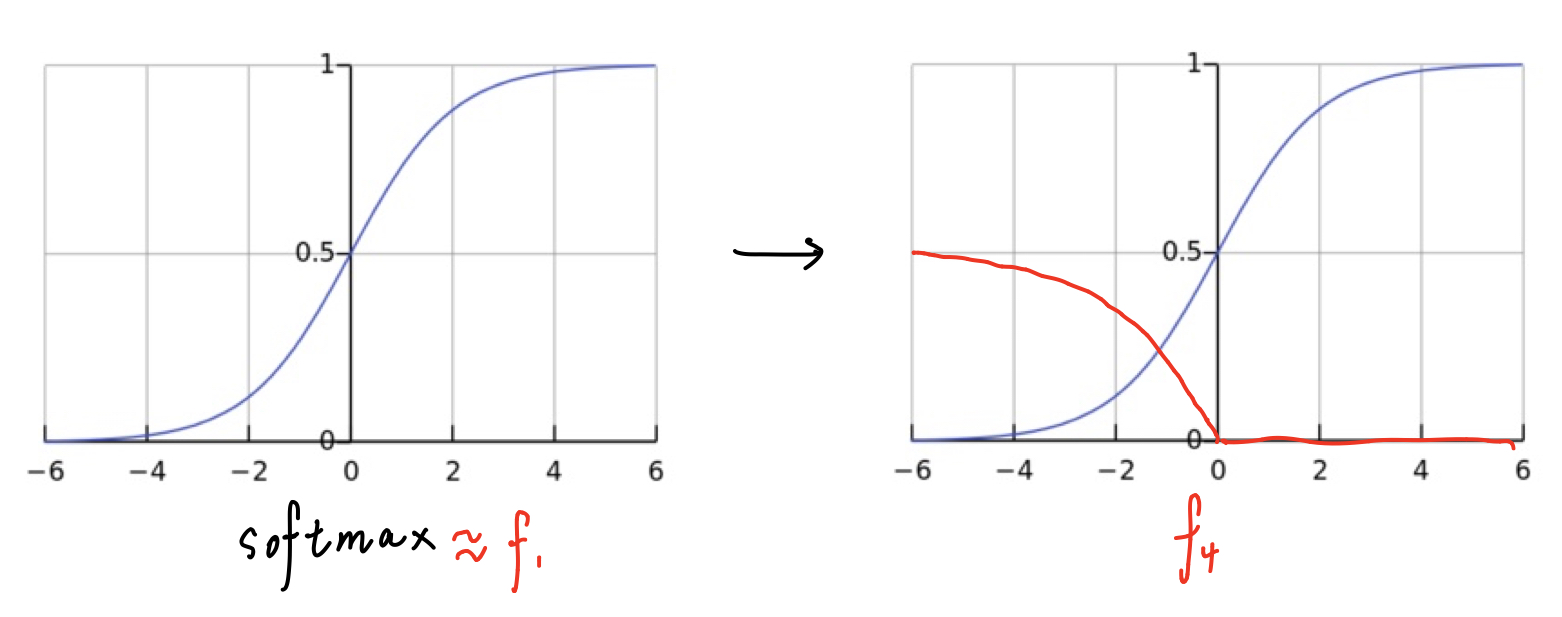
为了使梯度下降攻击在一开始发生变化，常数 $c$ 必须足够大

$$\epsilon\lt c(f_1(x+\epsilon)-f_1(x))$$

或者当攻击快结束时，即 $\epsilon \rightarrow 0$，有

$$\frac{1}{c}\lt|\nabla f_1(x)|$$

意味着 $c$ 一定要比梯度的倒数更大。

以下为个人对论文的理解：对于 $f_1$ 而言，交叉熵损失函数长得很像 softmax，所以攻击开始的时候呢，它的梯度很小，意味着 $c$ 非常的大，但是，当它逐渐增加的时候，梯度以指数的速度增加，这时候使得数值非常大且固定的 $c$ 表现得过度贪婪，即过度优化 $f_1$ 而忽略了 $D$，最终导致优化效果不好，$f_4$ 同理。那么对于 $f_6$，由于$Z(.)_t$的值基本是线性的，所以 $|\nabla f_6|$ 是一个常数，所以可以很好的找到一个固定的 $c$，所以不难解释为什么 $f_6$ 表现的比其他的好。

Discretization

对于有的图片，其像素数值是整数，则需要对攻击后的图像数据取整，即进行离散化，论文用的是贪心网格搜索。

Three Attacks

最后论文对$L_2$、$L_0$、$L_\infty$三种约束提出了三种攻击方法。

$L_2$ Attack

$$\text{minimize}\;||\frac{1}{2}(tanh(\omega)+1)-x||^2_2+c\,·\,f(\frac{1}{2}(tanh(\omega)+1)\\ f(x')=\text{max}(\max{\{Z(x')_i:i\ne t\}-Z(x')_t,-κ})$$

$f(x’)$ 这个函数用所有非目标标签的logit中最大值减去目标标签的logit，意味着，如果 $x’$ 被识别到目标标签，那么 $\max\{Z(x')_i:i\ne t\}-Z(x')_t$ 是负的，假如 $κ=0$，则$f(x')=0$，意味着该函数将不会被惩罚，否则如果 $x’$ 被识别到非目标标签，该函数将会受到惩罚。通过改变 $κ$ 值可以得到设想的置信度。

多起点梯度下降。梯度下降算法的主要问题是贪心搜索不能保证找到最优解，陷入局部极小值。为了弥补这一点，论文选择多个随机起点接近原始图像和运行梯度下降从每个点为固定次数的迭代。论文从半径为 $r$ 的球上均匀地随机采样点，其中 $r$ 是迄今为止发现的最接近的反例。从多个起点开始降低了梯度下降陷入一个糟糕的局部最小值的可能性。同时这也意味着 $L_2$ attack 可以并行化，从而可以提高攻击的速度。

$L_0$ Attack

由于 $L_0$ 距离度量是不能微分的，所以不能用标准梯度下降方进行求解。所以，论文使用迭代算法，在每次迭代中，识别出一些对分类器输出没有太大影响的像素，然后修复这些像素，因此它们的值永远不会改变。固定像素集在每次迭代中增长，直到通过消除过程确定了像素的最小子集(但可能不是最小子集)，可以修改该子集以生成对抗性示例。在每次迭代中，使用 $L_2$ attack 来识别哪些像素不重要。

具体来说，在每次迭代中，先调用 $L_2$ attack，只修改允许集中的像素，得到一个对抗样本，然后计算目标函数的梯度$g=\nabla f(x+\delta)$，选择这样的像素 $i=arg\,min_ig_i·\delta$，把它从允许集中剔除，原因是计算 $g_i·\delta_i$ 可以让我们知道通过扰动损失函数减少了多少，直到 $L_2$ attack 找不到对抗样本为止。

另一个细节就是 $c$ 的选取，最初将 $c$ 设为一个非常低的值(例如，$10^{−4}$)。然后用这个 $c$ 值来产生对抗样本。如果失败了，则将 $c$ 加倍，然后再试一次，直到成功为止。如果 $c$ 超过一个固定的阈值(例如，$10^{10}$)，则中止搜索。

整个算法与 JSMA 算法有些相似，JSMA增加了一组允许更改的像素(最初为空)，并设置像素以使总损失最大化。相反，$L_0$ attack 缩小了允许更改的像素集(最初包含每个像素)。论文提到，在每次迭代中，其不是从初始图像开始梯度下降，而是从上一个迭代中找到的解决方案开始梯度下降，这相当于“暖启动”，这极大地减少了每次迭代所需的梯度下降轮数，因为 $k$ 像素保持不变的解决方案通常与 $k + 1$ 像素保持不变的解决方案非常相似。

$L_{\infty}$ Attack

同样由于 $L_{\infty}$ 距离度量是不能微分的，所以不能用标准梯度下降方进行求解。论文一开始直接对下式进行优化：

$$\text{minimize}\;c\,·\,f(x+\delta)+||\delta||_\infty$$

但是实验结果表明 $||\delta||_\infty$ 项只对扰动最大的像素点进行惩罚，而对其他像素点没有影响。论文使用迭代攻击来解决这个问题，通过引入一个递减的阈值 $\tau$，如果扰动 $\delta_i$ 大于该值则目标函数将会被惩罚，直到所有扰动都小于该阈值为止：

$$\text{minimize}\;c\,·\,f(x+\delta)+\sum_i[(\delta_i-\tau)^+]$$

在每次迭代中使用“暖启动”来进行梯度下降，该算法的速度大约与$L_2$ attack算法一样快(只有一个起始点的时候)。另外 $c$ 值选取的策略和 $L_0$ attack 一致。

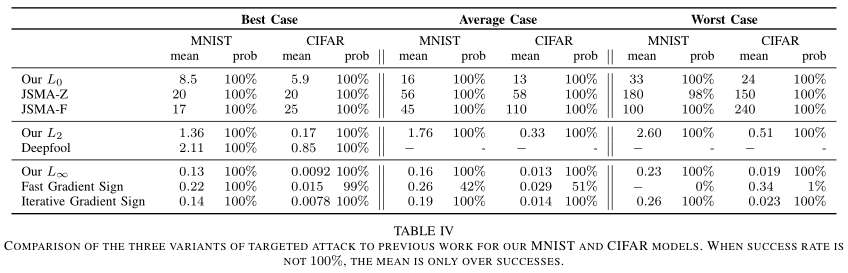
可以看到三种攻击方法的性能比前面做的还是有很大的提升。

Evaluating Defensive Distillation

蒸馏网络原来是神经网络压缩的一种方法，蒸馏网络的直觉是基于这样的一个事实，即在训练过程中DNN获得的知识不仅被编码为DNN学习的权重参数，而且还被编码为网络产生的概率向量。使用类别概率代替硬标签的好处是直观的，因为概率除了简单提供样本的正确类别外，还会编码有关每个类别的其他信息，可以从这个额外的熵推导出有关类的相对信息。

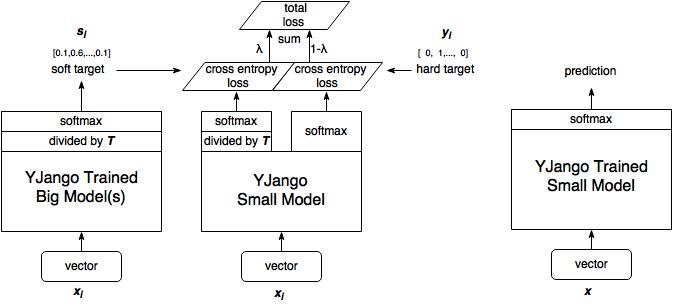
蒸馏网络的训练步骤：

1. 训练大型模型：首先训练具有硬目标即正常标签(单标签)的大型模型。
2. 计算软目标：使用训练有素的大型模型来计算软目标。 也就是说，大型模型“软化”后，将通过softmax的输出。
3. 训练小模型，在小模型的基础上添加附加的软目标损失函数，并通过 $\lambda$ 调整两个损失函数的比例。
4. 进行预测时，以常规方式使用训练好的小模型（右图）。

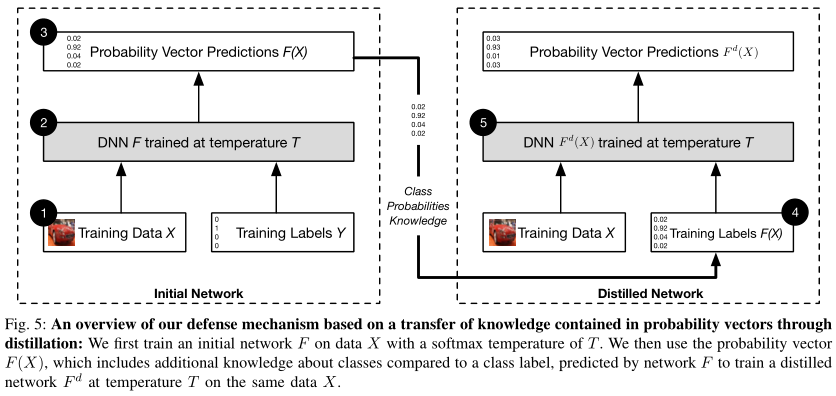
训练防御性蒸馏网络步骤如下：

1. 在硬标签的监督下训练教师模型。

2. 训练完后，使用教师模型来计算得到软标签，具体而言：

   $$q_i=\frac{exp(z_i/T)}{\sum_jexp(z_i/T)}$$

3. 在软标签的监督下训练学生模型，这个学生模型与教师模型有着相同的形状。

4. 进行预测的时候，学生模型以常规方式进行预测，即 $T=1$。

两种训练的主要区别我认为一个是学生模型的规模，另一个是 $\lambda$ 的设置是否。

在软标签的计算中，参数 $T$ 是一个超参数，$T$ 越大，曲线越平滑，这意味着教师模型以较大的 $T$ 来训练网络可以产生分布更加均匀的软标签，随后学生模型以同样的 $T$ 进行学习，可以更加容易学习到类之间的相对信息。在最终预测中，重新设置 $T=1$，这有利于正确类别以高置信度胜出，而错误类别输出的置信度很低，此时 softmax 层本质上输出了一个硬标签。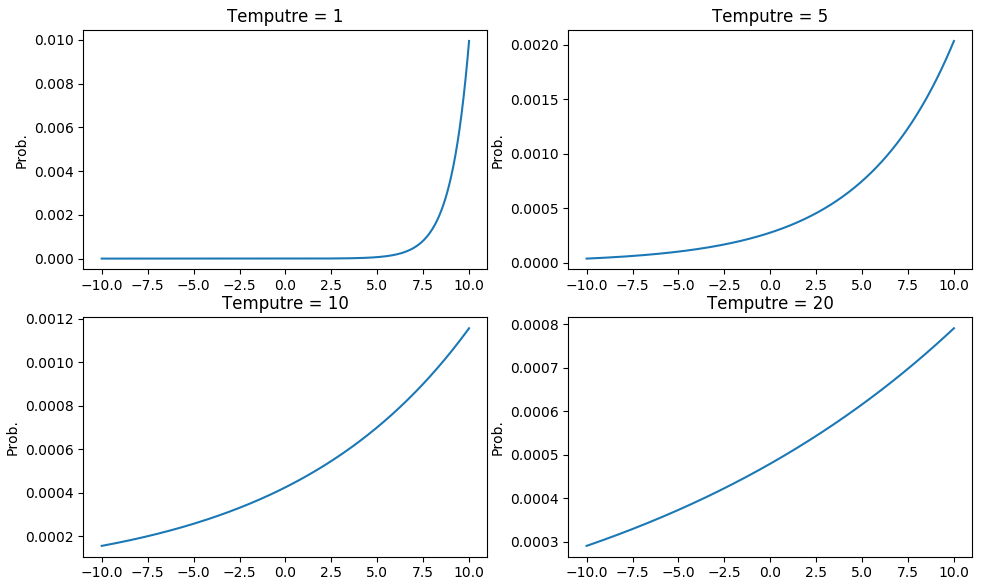

这篇论文提到，事实上，在大多数情况下错误类别输出的置信度太小，以至于32位浮点值四舍五入为0。出于类似的原因，梯度非常小，当用32位浮点值表示时，梯度就变成了0。这导致了依赖于以错误类别梯度进行攻击的算法（FGSM）和依赖梯度进行优化（L-BFGS）或迭代（JSMA-F）的攻击算法由于梯度消失而失效。（JSMA-Z）也会失效是因为改变目标分类所需要相对的差异在 $T= 1$ 很大，比如当 logit 从 -100 到 -90，输出仍然是原来的分类，而当 logit 从 10 到 0，输出却变成了另一个类别。

论文评估了本文提出的三种攻击在防御性蒸馏网络效果，如下图，可以看出成功率都为100%。

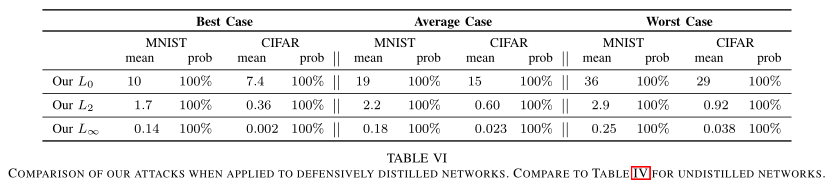
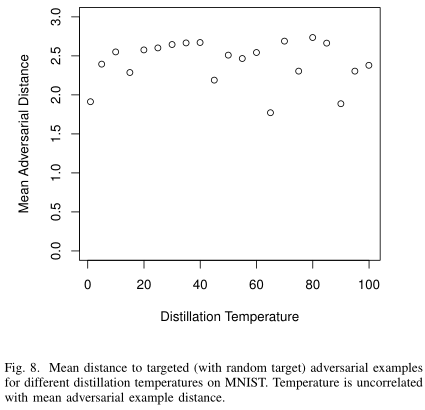
另外在以往的工作中，提高蒸馏网络的温度 $T$ 会降低攻击的成功率，而实验显示，$L_2$ attack 成功率与 $T$ 是不相关的，这意味着攻击方法是鲁棒的。

一个模型的对抗样本往往也能对另一个模型攻击成功，即使它们在不同的训练数据集上训练，即使它们使用完全不同的算法(神经网络上的对抗样本攻击随机森林），这称为对抗样本攻击迁移性，论文分别在非蒸馏网络和防御性蒸馏网络中评估攻击的迁移性能。

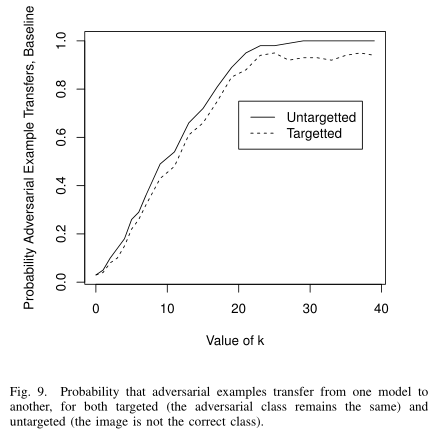
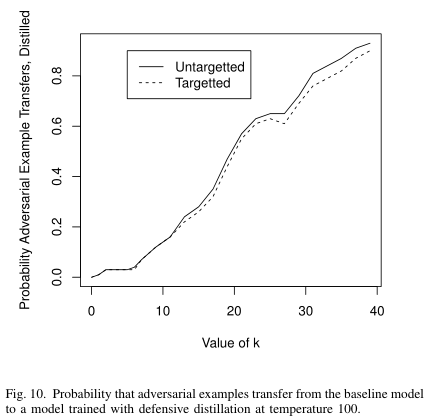
在 $L_2$ attack 中，$f(x')=\text{max}(\max{\{Z(x')_i:i\ne t\}-Z(x')_t,-κ})$，其中 $κ$ 值用于控制对抗样本的强度， $κ$ 值越大，对抗样本的置信度越高。从图中看出，高置信度的对抗样本迁移性越强。当然使用了防御性蒸馏的网络在一定程度上可以抵御对抗样本的迁移攻击。因此作者认为通过使更强的攻击算法和迁移攻击的成功率来评估神经网络防御的鲁棒性。

[参考资料]

1. https://blog.csdn.net/paper_reader/article/details/81080857
2. https://blog.csdn.net/nature553863/article/details/80568658
3. https://www.bilibili.com/read/cv4009730
4. https://blog.csdn.net/jmh1996/article/details/101635216
5. https://www.bilibili.com/video/av66382805/
6. https://blog.csdn.net/kearney1995/article/details/79904095