以一种直观的方式理解扩散生成模型

1. 本人是在 2023 年 5 月份开始学习相关论文，主要面向图像复原相关下游应用的预研工作，全职研究时间大约三个月，不算很长，认识有限。
2. 写本博客的初衷是为了结构化一下之前学习的知识网络，如果看到外部链接的话就是在串接知识网络（从下一行就开始了），或许介绍一种或许更容易入门理解的方式（论文阅读顺序）。
3. 本博客需要一定的数学基础，如果想了解 stable-diffusion-webui 或者 ComfyUI 的使用方法请绕路。
4. 当然真正的勇士也可以像笔者之前一样直面惨淡的数学原理，当然也可以看本博客娓娓道来胡说八道。
5. 可能会以一种不太严谨的方式表达想表达意思，希望能多多包涵，不喜轻喷，也欢迎一起讨论！

自 DDPM[1]被提出来之后，到目前 Stable Diffusion[2] 已经成为主导整个开源社区的文生图模型。对于想真正探讨扩散模型背后原理的童鞋来说，一方面由于模型的高易用性和开源工具的快速发展降低了模型的使用门槛，大量的博客在介绍开源工具的使用方法，这增大了相关匹配知识的检索难度；另一方面，真正介绍扩散模型背后原理的论文和博客又容易过于数学公式化，让人晦涩难懂（以至于笔者也没有完全搞懂所有知识）。因此本文想写一篇介于两者之间，或许更偏向于后者的博文。本人对主要的high-level认识来源还是来自于 Song Yang 博士的博客和讲解，当然一开始看的时候我并没有完全看懂他想表达的意思，也是反复咀嚼了很多，在此记录一下我的二次理解。

一个直观感受

在已有的主流图像生成模型中，无论是大家熟知的VAE[3]、GAN[4]，还是相对鲜为人知Autoregressive Model[5]，Flow-based Generative Model[6]，不管它们内部模型细节，都可以将这些模型宏观抽象为输入$x$到输出$y$的映射$y=f_\theta(x)$，其中$f_\theta(.)$为对应的映射函数，在神经网络中，往往看成是一种从数据中统计学习出来的非线性映射。

想象一下，如果这个模型被建模为一个迭代式模型，需要经过 $T$ 次映射而不是原来的一次映射就能得到结果，给定初始输入$x_T$，经过 $T$ 次不同的映射得到 $y$，这个过程可以公式化为：

$$\begin{align*} x_{T-1}&=f_{\theta_T}(x_T) \\ x_{T-2}&=f_{\theta_{T-1}}(x_{T-1}) \\ \vdots \\ x_t&=f_{\theta_{t-1}}(x_{t-1}) \\ \vdots \\ y&=f_{\theta_{1}}(x_{1}) \\ \end{align*}$$

这可以理解为我们从将原来映射函数的一步到位，分解为 $T$ 次映射，这降低了单次映射函数的学习难度，也增加了整个模型的表达能力。我们可以把当前迭代次数也作为映射函数输入的一部分，这样在实际中，我们可以只需要保存一次相关参数：

$$x_{t-1}=f_{\theta}(x_{t},t) \\$$

进一步地想象，如果这个迭代式模型并不是直接将 $x_i$ 映射到 $x_{i+1}$，而是计算它俩之间的差异，为了区分于 $f_\theta(.)$，这里用 $h_\theta(.)$ 来表示差异项，原来的映射关系可以公式化为：

$$x_{t-1}=x_{t}-h_\theta(x_{t},t)$$

上面公式粗略一看，这不类似于神经网络中常用的Residual Network的公式表达吗？事实上，扩散模型的生成过程就是可以被这样个公式抽象表达。原来定义的 $t$ 是一个离散的标量，更一般地，我们可以建模为连续的关系，可以认为有无穷个小的网络映射，其中 $dt$ 看成是一个很小的变化：

$$x_t=x_{t-dt}-h_\theta(x_{t-dt},t-dt)$$

上式可以写成一个导数的形式：

$$\frac{dx_t}{dt}=-h_\theta(x_{t-dt},t-dt)$$

其中，$\frac{dx_t}{dt}$ 是 $x_t$ 关于 $t$ 的导数。我们已知初态 $x_T$，和导数项 $\frac{dx_t}{dt}$，这可以看成是常微分方程的初值问题。这意味着我们常用的端到端神经网络的一次映射计算结果，可以转换为使用常微分方程优化器(ODE Solver)进行求解[7]（头好痒，要长脑子了吗？）。

欧拉方法

这里我参考了[8] [9]中的的教程，Euler’s Method是一种数值方法，其基本思想很简单，就是用折线逼近曲线。下图中描述的是Euler’s Method的基本原理：给定一个初态 $x_0=x(t_0)$和 $x_t$ 关于 $t$ 的导数$\frac{dx_t}{dt}=h(x_t,t)$，迭代步长为 $\Delta t$，经过 $n$ 次迭代，能逐渐迭代逼近最终的真实值。

以一个案例来说明Euler’s Method的过程，给定一个待估计真实函数映射 $x_t=t^2$，我们的目的是当 $t = 1.5$ 时，估计当前函数的值，已知初始状态 $t_0=1$ 和$x_t$ 关于 $t$ 的每个点的导数 $\frac{dx_t}{dt}=h(x_t,t)=2t$，现在变化一个很小的步长 $\Delta t$，理论上这个步长越小逼近程度越精准，但代价是算法迭代速度随着步长减小而变慢，这里为了演示算法案例取 $\Delta t=0.1$。

从物理意义上来理解，$\frac{dx_t}{dt}$ 描述地是每变化很小 $dt$，$x_t$ 的变化程度是 $dx_t$。

• 假定在 $n=0$的时候，$t_0=1$，此时 $h_0(x_t,t)=2t_0=2$，

• 进行第一次迭代，$n=1$，此时$t_1=t_0+\Delta t=1.1$，$h_1(x_t,t)=2t_1=2.2$，估计结果$\hat{x}_{t_1}=x_{t_0}+\Delta t\cdot h_0(x_t,t)=1.2$；

• 进行第二次迭代，$n=2$，此时$t_2=t_1+\Delta t=1.2$，$h_2(x_t,t)=2t_2=2.4$，估计结果$\hat{x}_{t_2}=x_{t_1}+\Delta t\cdot h_1(x_t,t)=1.42$；
• 类似地，经过多次迭代后，我们来到 $n=5$，此时 $t_5=1.5$，估计结果$\hat{x}_{t_5}=x_{t_4}+\Delta t\cdot h_4(x_{t},t)=2.2$，真实结果是$x_{t_5}={t_5}^2=2.25$，可以看到两者非常逼近。

当然，为了不偏离我们的主题，此处仅介绍Euler-Maruyama method这样一种一阶常微分方程优化器的案例，后续有许多基于类似思想的常微分方程优化器如Milstein method、stochastic Runge-Kutta methods)等，提供更加精准和速度更快地估计，更一般地可以拓展到随机微分方程优化器中，此处就不再赘述。

回到DDPM

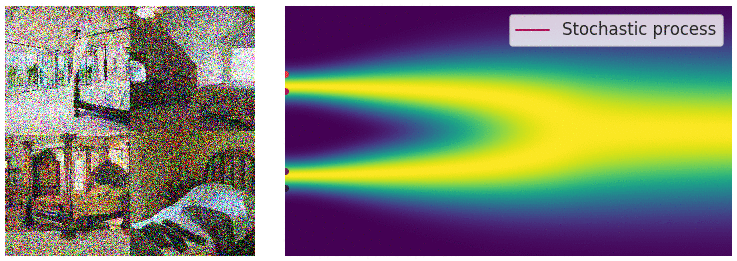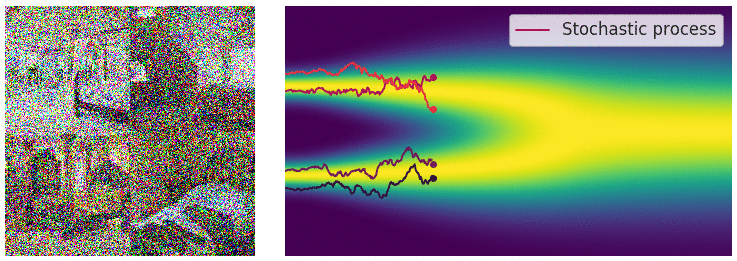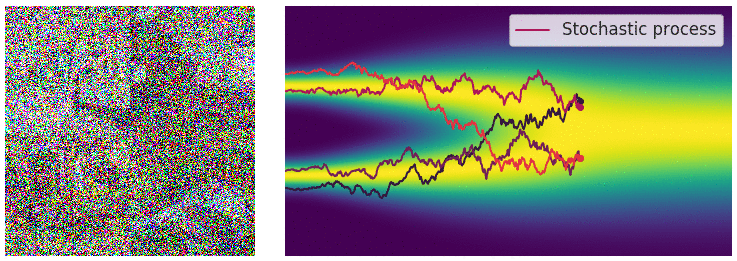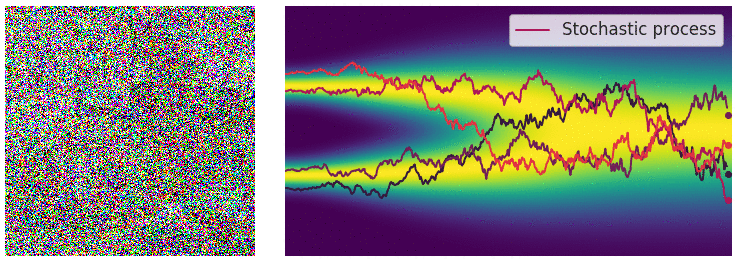
扩散生成模型的运作的童鞋都知道，其分为前向和后向两个过程，其中前向过程是指给数据集采样的图像逐渐地添加高斯噪声，直至图像信号渐渐被噪声覆盖，而变成一个高斯噪声图为止，这个过程可以看成是一个随机过程：

$$dx=f(x_t,t)dt+g(t)dw_t$$

其中，$dt$是一个正无穷小的时间步长，$dx$表示随机过程 $x_t$ 在时间 $dt$ 的微小增量，$w_t$ 是标准布朗运动，$dw_t\sim N(0,dt)$可以看成是一个无穷小的白噪声。这里的 $f(x_t,t)$ 可以看成图像信号，是一个已知的函数，$g(t)$ 可以看成是人工设定的参数，可以看成是信噪比系数，表示噪声水平，该公式的解读意义是每次扩散的前向过程是基于图像信息以一个人工设定的噪声扰动进行的。

更重要地是，任何随机微分方程都有他对应的一个逆随机微分方程[10]，这个推导需要较多的数学功底，此处略去，直接给出它的形式是：

$$dx=[f(x,t)-g^2(t)\nabla_x \log p_t(x)]dt+g(t)dw_t$$

这里的 $dt$ 是一个负无穷小的时间步长，其他符号含义与上述一致，而比较难以解释的是 $\nabla_x \log p_t(x)$ 这一项，在Song Yang的score matching系列[11][12]工作中，该项也叫得分函数（score function），当然这个概念在更早的工作中被提出[13][14]，最后，在Song Yang[15]的工作中，将score-based model和DDPM统一起来。先来看看该项的数学含义是，在某个迭代时刻 $t$，该时刻的对数概率密度函数 $p_t(x)$ 关于 $x$ 的梯度（头好痒，要长脑子了吗？）。

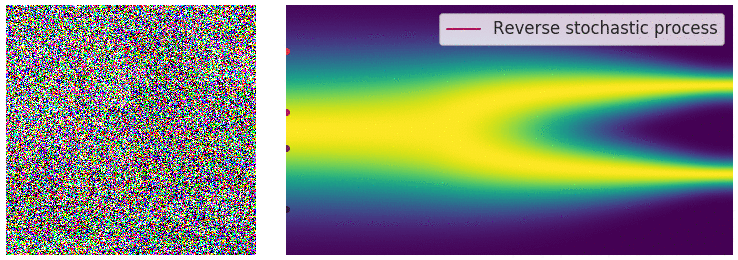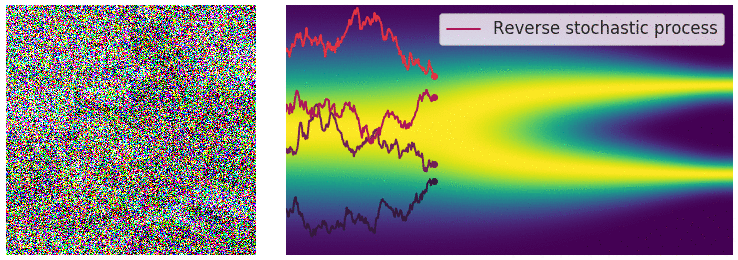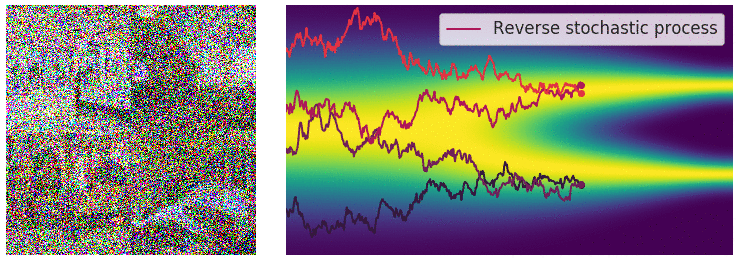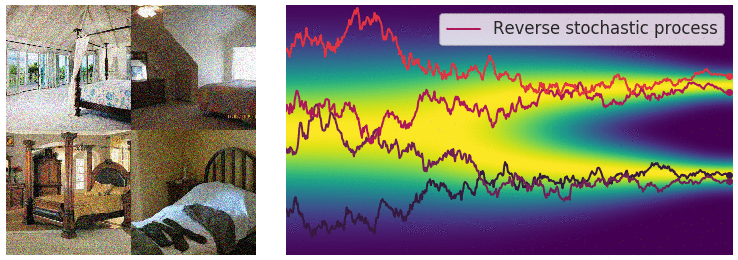
Well…在深入讨论算法细节和含义之前，我们可以先回到上帝视角来从High-level思考这个问题。前面知道前向过程是一个人工设定的一个确定性过程，但实际上我们想达成的任务目标是图像生成，根据逆随机微分方程，如果在扩散模型逆向过程，我们已知$f(x,t)、g(t)、dt$和$dw_t$的分布，如果能知道 $\nabla_x \log p_t(x)$ 这一项，就能计算得到 $dx$，最后迭代地做到图像生成。

此时，可以联想到前面讲的，常微分方程的数值求解过程，可以发现两者均是利用梯度。但是不同的是，在上面常微分方程的数值求解过程中，给定了一个初始状态和梯度，这个梯度描述的是当前状态到下一状态的变化趋势；而在逆随机微分方程中，其梯度想要描述的状态不仅是一个点的状态，而是一群点的状态，也就是分布。即给定一个初始分布和梯度，这个梯度描述是的当前阶段分布到下一阶段分布的变化趋势。

这里为什么要用分布而不是用点？我理解相关工作在开始研究的时候出于生成图像分布多样性的考虑，纵使以高斯噪声初始化有一定的多样属性，但随着固定的点的梯度迭代转换到最终状态，直观感受下这样的做法会使最终图像分布多样性大打折扣，但事实上后续的扩散生成研究工作中也有很多使用常微分方程优化器的生成方法(sampling method)。

对于常微分方程的初值问题，可以沿着其梯度方向移动，当梯度趋近于0的时候，可以获得一个局部最优点；而在逆随机微分方程的视角中，如下图所示，蓝色点是初始（先验）分布上随机采样的点，类似的，沿着分布的梯度 $dx$ 方向移动，当梯度趋近于0的时候（图中箭头长度短），我们得到的是什么呢？它是当前时刻，分布的局部最优点，也就是数据分布概率密度函数最大的地方，或者用另一套说法就是，梯度的方向指向了数据分布概率密度函数的地方。哪个位置是数据分布概率密度函数最大？这取决于我们训练使用的分布情况，在扩散图像生成的应用中，就是训练的中使用的要生成的图像分布。

回到 DDPM，对于时间独立的对数概率密度函数 $\nabla_x \log p_t(x)$ ，我们并不能直接获得它的解析解，但是我们可以通过给定一个数据分布，通过训练来近似得到这个表达，在score-based model 系列论文中，网络的优化目标为：

$$E_{p(x)}[||\nabla_x\log p(x)-s_\theta(x)||^2_2]=\int p(x)||\nabla_x \log p(x)-s_\theta(x)||^2_2dx$$

这个式子也叫Fisher divergence，和KL-divergence类似可以理解为分布逼近损失。其中左式是期望的写法，右式是积分的写法，$s_\theta(x)$网络的输出（这个式子中，$t$ 参数被省略），但这里比较难理解的是，$\nabla_x \log p(x)$ 对应到训练中是什么形式，这不像以往端到端图像复原任务中有一个高质图像作为Ground Truth就是我们的优化目标，在扩散生成模型的上下文中，什么是我们的优化目标？

这里就要回到构造数据的前向过程中，省略的构造细节，虽然有很多种加噪逻辑（noise scheduler），当每次加噪水平无穷小，加噪次数无穷大的时候，每次添加的高斯噪声就可以看成是前向过程的分布梯度项，反过来就是逆向过程的分布梯度项 $\nabla_x \log p(x)$，这里在网络优化的过程中并不需要显示建模对数项，因为网络本身就能cover这样的非线性。我想表达的是：前向加噪的过程就是在人为地设计分布梯度项，人为地定义了时间独立 $t$ 时刻的优化目标。另外，网络的优化目标并不需要显示地建模期望，因为每epoch在数据集上采样训练就是在隐式地建模了概率密度函数 $p(x)$。网络训练收敛后，就意味着我们可以得到时间独立的对数概率密度函数 $\nabla_x \log p_t(x)$ 的估计，利用逆随机微分方程的公式，给定初始先验分布$p_T(x)$，在上面采样一个样本点 $f(x,T)$，和预先设定的噪声水平 $g(t)$，计算得到当前时刻 $T$ 的逆向梯度 $dx$，利用优化器（Solver）将该样本点移动到训练数据所在分布上。

这大概是我对这个模型一些直观和浅显的理解，以后有空再深入探讨数学原理。

参考：

[1] Denoising Diffusion Probabilistic Models.

[2] High-Resolution Image Synthesis with Latent Diffusion Models.

[3] VAE: Auto-Encoding Variational Bayes.

[4] Generative Adversarial Network.

[5] Maximum Likelihood Training of Score-Based Diffusion Models.

[6] Glow: Generative Flow with Invertible 1×1 Convolutions.

[7] Neural Ordinary Differential Equations.

[8] Euler method | Lecture 48 | Numerical Methods for Engineers

[9] Euler’s Method Differential Equations, Examples, Numerical Methods, Calculus.

[10] Reverse-time diffusion equation models.

[11] A connection between score matching and denoising autoencoders.

[12] Sliced score matching: A scalable approach to density and score estimation.

[13] Estimation of non-normalized statistical models by score matching.

[14] A connection between score matching and denoising autoencoders.

[15] Score-Based Generative Modeling through Stochastic Differential Equations.