逗比学长的博客

此人有“亿”点强迫症

图形算法Plug and play

发表于 更新于 阅读次数：

矩阵

标准化矩阵

  1. 遍历矩阵每列求特征的平均值。
  2. 遍历矩阵每个元素减去该列的平均值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Mat<T> normalize() {
    std::vector<double>colWiseMean(m_col);
    for (size_t col = 0; col < this->m_col; col++) {
        double mean = 0.0;
        for (size_t row = 0; row < this->m_row; row++) {
            mean += (*this)[row][col];
        }
        colWiseMean[col] = mean / this->m_row;
    }

    for (size_t row = 0; row < this->m_row; row++) {
        for (size_t col = 0; col < this->m_col; col++) {
            (*this)[row][col] -= colWiseMean[col];
        }
    }
    return *this;
}

矩阵变换(可看做modelMatrix)

平移

1
2
3
4
5
6
7
Matrix translation(Vec3f v) {
	Matrix Tr = Matrix::identity(4);
	Tr[0][3] = v.x;
	Tr[1][3] = v.y;
	Tr[2][3] = v.z;
	return Tr;
}

缩放

1
2
3
4
5
Matrix zoom(float factor) {
	Matrix Z = Matrix::identity(4);
	Z[0][0] = Z[1][1] = Z[2][2] = factor;
	return Z;
}

旋转

绕x轴旋转：

1
2
3
4
5
6
7
Matrix rotation_x(float cosangle, float sinangle) {
	Matrix R = Matrix::identity(4);
	R[1][1] = R[2][2] = cosangle;
	R[1][2] = -sinangle;
	R[2][1] = sinangle;
	return R;
}

绕y轴旋转

1
2
3
4
5
6
7
Matrix rotation_y(float cosangle, float sinangle) {
	Matrix R = Matrix::identity(4);
	R[0][0] = R[2][2] = cosangle;
	R[0][2] = sinangle;
	R[2][0] = -sinangle;
	return R;
}
1
2
3
4
5
6
7
Matrix rotation_z(float cosangle, float sinangle) {
	Matrix R = Matrix::identity(4);
	R[0][0] = R[1][1] = cosangle;
	R[0][1] = -sinangle;
	R[1][0] = sinangle;
	return R;
}

绕任意轴旋转

视图矩阵(viewMatrix)

类似于glm的视线，输入相机所在位置eye，相机照向的中心点位置center，相机的上向量up，一般为Vec3(0,1,0)：

代码自TinyRender Lesson 5：

1
2
3
4
5
6
7
8
9
10
11
12
13
Matrix lookat(Vec3f eye, Vec3f center, Vec3f up) {
	Vec3f z = (eye - center).normalize();
	Vec3f x = (up ^ z).normalize();
	Vec3f y = (z ^ x).normalize();
	Matrix res = Matrix::identity(4);
	for (int i = 0; i < 3; i++) {
		res[0][i] = x[i];
		res[1][i] = y[i];
		res[2][i] = z[i];
		res[i][3] = -center[i];
	}
	return res;
}

透视矩阵(ProjectionMatrix)

代码来自kimi：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
float fovY = 45.0f * static_cast<float>(M_PI / 180.0f); // 45度转换为弧度
float aspectRatio = 16.0f / 9.0f; // 屏幕宽高比
float zNear = 0.1f; // 近裁剪面
float zFar = 100.0f; // 远裁剪面
template <typename T>
mat4<T> perspective(T fovY, T aspectRatio, T zNear, T zFar) {
    T f = 1.0f / tan(fovY / 2.0f);
    T range = zFar - zNear;

    mat4<T> projMatrix(
        f / aspectRatio, 0.0f, 0.0f, 0.0f,
        0.0f, f, 0.0f, 0.0f,
        0.0f, 0.0f, -(zFar + zNear) / range, -1.0f,
        0.0f, 0.0f, -2.0f * zNear * zFar / range, 0.0f
    );

    return projMatrix;
}

视口变换(viewPort)

代码自TinyRender Lesson 5：

1
2
3
4
5
6
7
8
9
10
11
Matrix viewport(int x, int y, int w, int h) {
    Matrix m = Matrix::identity(4);
    m[0][3] = x+w/2.f;
    m[1][3] = y+h/2.f;
    m[2][3] = depth/2.f;

    m[0][0] = w/2.f;
    m[1][1] = h/2.f;
    m[2][2] = depth/2.f;
    return m;
}

这个代码用于创建以下矩阵，其将坐标从 [-1,1]*[-1,1]*[-1,1] 被映射到屏幕立方体 [x,x+w]*[y,y+h]*[0,d] 上，其中d 是 z 缓冲区的分辨率。可以使其等于 255，因为这样可以方便地转储 z 缓冲区的黑白图像以进行调试。

协方差矩阵

  1. 矩阵的转置乘以该矩阵。
  2. 有偏估计？
1
2
3
4
5
6
7
8
9
Mat<T> covariance() {
    Mat<T> res = this->transpose().matmul(*this);
    if (this->m_row < 2) {
        std::cout << "Dim" << std::endl;
        exit(-1);
    }
    res = res.mul(1.0 / (this->m_row - 1));
    return res;
}

矩阵的行列式

  1. 递归式调用求取子矩阵的行列式。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
T determinant() {
    if (this->m_row != this->m_col) {
        std::cerr << "Error: Determinant can only be calculated for square matrices." << std::endl;
        return 0.0;
    }

    if (this->m_row == 1) {
        return (*this)[0][0];
    }

    double det = 0.0;
    int sign = 1;

    for (size_t i = 0; i < this->m_row; i++) {
        Mat<T> submat = submatrix(0, i);
        det += sign * (*this)[0][i] * submat.determinant();
        sign = -sign;
    }

    return det;
}

Mat<T> submatrix(size_t row, size_t col) {
    Mat<T> submat;
    for (size_t i = 0; i < this->m_row; i++) {
        if (i == row) continue;
        std::vector<T> subrow;
        for (size_t j = 0; j < this->m_col; j++) {
            if (j == col) continue;
            subrow.push_back((*this)[i][j]);
        }
        submat.push_back(subrow);
    }
    return submat;
}

矩阵的特征值和特征向量

求解PCA协方差矩阵的特征值和特征向量可以表达成矩阵特征值问题的标准形式AX = λX，其中A是协方差矩阵，X是特征向量矩阵，λ是特征值矩阵。

我们可以将这个问题转化为标准形式AX = B，其中A = A，X是一个矩阵，每一列是特征向量v，B是一个矩阵，每一列是对应的特征值λ。

因此，通过求解矩阵特征值问题的标准形式AX = λX，我们可以得到PCA协方差矩阵的特征值和特征向量。

雅克比(Jacobi)迭代法

参考：https://blog.csdn.net/Reborn_Lee/article/details/80959509

一般形式

方程组：

的系数矩阵$A$非奇异，不妨设，方程组变形为

对应上述的方程组，可得到迭代公式为：

其中，为第 $k$ 次迭代向量。

一般形式代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>

using namespace std;

vector<double> jacobiIteration(vector<vector<double>> A, vector<double> b, int max_iter, double tol) {
    int n = A.size();
    vector<double> x(n, 0.0);
    vector<double> x_new(n, 0.0);
    int iter = 0;

    while (iter < max_iter) {
        for (int i = 0; i < n; i++) {
            double sum = 0.0;
            for (int j = 0; j < n; j++) {
                if (j != i) {
                    sum += A[i][j] * x[j];
                }
            }
            x_new[i] = (b[i] - sum) / A[i][i];
        }

        double error = 0.0;
        for (int i = 0; i < n; i++) {
            error += abs(x_new[i] - x[i]);
        }

        if (error < tol) {
            break;
        }

        x = x_new;
        iter++;
    }

    return x;
}

int main() {
    vector<vector<double>> A = {{4, -1, 0},
                                 {-1, 4, -1},
                                 {0, -1, 4}};
    vector<double> b = {8, 7, 6};
    int max_iter = 100;
    double tol = 1e-6;

    vector<double> solution = jacobiIteration(A, b, max_iter, tol);

    cout << "Solution: ";
    for (int i = 0; i < solution.size(); i++) {
        cout << solution[i] << " ";
    }
    cout << endl;

    return 0;
}

矩阵形式:

形如 AX=b 的方程组求解：

其中 $A$ 非奇异且 . 将 $A$ 分裂为 $A=D+L+U$，其中

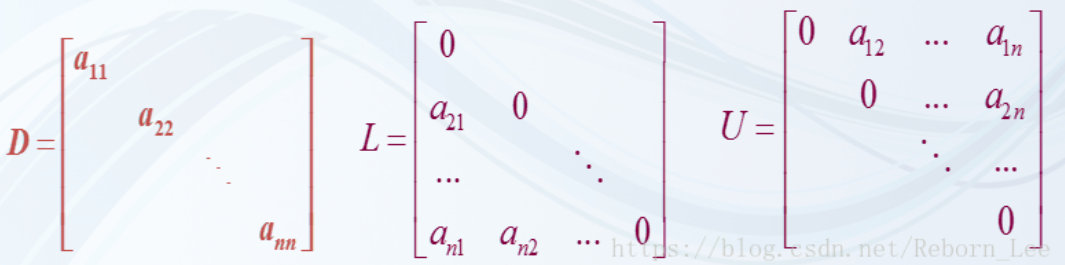
JacobiIteration

因此可以将 Ax=b 表示为 Dx=-(L+U)x+b)，即 ，简记为 ，因此Jacobi迭代公式的矩阵形式为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
std::vector<T> JacobiIteration(const Mat<T>& A, const std::vector<T>& b, int max_iter = 100, T tol = 1e-6) {
    Mat<T> D_inv = GetDInv(A);
    Mat<T> L = GetL(A);
    Mat<T> U = GetU(A);
    Mat<T> LplusU = L + U;
    Mat<T> B = -D_inv.matmul(LplusU);
    std::vector<T> d = Mat::MatrixMultiplyVector(D_inv, b);
    std::vector<T> x(d.size(), 0.0);
    std::vector<T> x_new(d.size(), 0.0);
    Mat<T> res;

    int iter = 0;

    while (iter < max_iter) {
        std::vector<T> Bx = Mat::MatrixMultiplyVector(B, x);
        x_new = Mat::VectorAdd(Bx, d);
        T error = Mat::AbsDist(x, x_new);

        if (error < tol) {
            break;
        }

        x = x_new;
        iter++;
    }
    return x;
}

图形学

OBJ解析

原文链接：https://blog.csdn.net/xiongzai2016/article/details/108052800

现在来解释各参数的含义：

  • v: 表示顶点。
  • vt: 纹理坐标，其值为u, v。
  • vn：顶点法向量，其值为x,y,z。
  • f：表示一个面，由三个v/vt/vn的索引形式组成。比如obj文件中f 5/15/7 4/14/6 6/16/8 ，表示由第5、第4、第6这三个顶点组成了一个三角平面,平面的纹理由第15、第14、第16这三个纹理坐标形成，这个平面的朝向是第7、第6、第8这三个顶点的法向量求平均值。

绘制直线

Bresenham’s line算法：

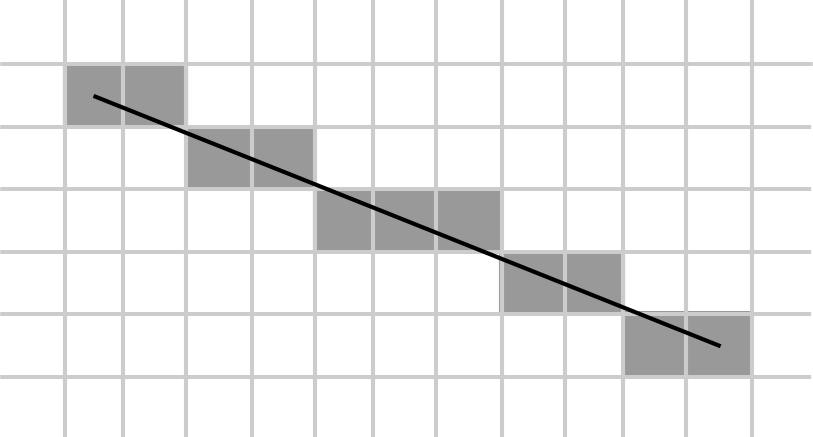
图自Bresenham wikipedia

代码自tinyrenderer, Lesson1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void line(int x0, int y0, int x1, int y1, TGAImage& image, TGAColor color) {
    bool steep = false;
    // 为了遍历斜率小于0.5的轴，每次遍历轴自增1，而另一个轴自增小于1，防止某些点被miss
    if (std::abs(x0 - x1) < std::abs(y0 - y1)) {    
        std::swap(x0, y0);
        std::swap(x1, y1);
        steep = true;
    }
    if (x0 > x1) {    // 为了从左到右开始遍历
        std::swap(x0, x1);
        std::swap(y0, y1);
    }

    for (int x = x0; x <= x1; x++) {
        // 通过比例计算关系
        float t = (x - x0) / (float)(x1 - x0);
        int y = y0 * (1. - t) + y1 * t;
        if (steep) {
            image.set(y, x, color);
        }
        else {
            image.set(x, y, color);
        }
    }
}

上面的代码结合uv有些bug，下面ok，代码自tinyrenderer, Lesson4 final：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void triangle(Vec3i t0, Vec3i t1, Vec3i t2, Vec2i uv0, Vec2i uv1, Vec2i uv2, TGAImage& image, float intensity, int* zbuffer) {
	if (t0.y == t1.y && t0.y == t2.y) return; // i dont care about degenerate triangles
	if (t0.y > t1.y) { std::swap(t0, t1); std::swap(uv0, uv1); }
	if (t0.y > t2.y) { std::swap(t0, t2); std::swap(uv0, uv2); }
	if (t1.y > t2.y) { std::swap(t1, t2); std::swap(uv1, uv2); }

	int total_height = t2.y - t0.y + 1;
	for (int i = 0; i <= total_height; i++) {
		bool second_half = (i > t1.y - t0.y) || t1.y == t0.y;
		int segment_height = second_half ? (t2.y - t1.y + 1) : (t1.y - t0.y + 1);
		float alpha = (float)i / total_height;
		float beta = (float)(i - (second_half ? t1.y - t0.y : 0)) / segment_height;//  be careful: with above conditions no division by zero here
		Vec3i A = t0 + Vec3f(t2 - t0) * alpha;
		Vec3i B = second_half ? t1 + Vec3f(t2 - t1) * beta : t0 + Vec3f(t1 - t0) * beta;
		Vec2i uvA = uv0 + (uv2 - uv0) * alpha;
		Vec2i uvB = second_half ? uv1 + (uv2 - uv1) * beta : uv0 + (uv1 - uv0) * beta;
		if (A.x > B.x) { std::swap(A, B); std::swap(uvA, uvB); }
		for (int j = A.x; j <= B.x; j++) {
			float phi = B.x == A.x ? 1. : (float)(j - A.x + 1) / (float)(B.x - A.x + 1);
			Vec3i P = Vec3f(A) + Vec3f(B - A) * phi;
			Vec2i uvP = uvA + (uvB - uvA) * phi;
			int idx = P.x + P.y * width;
			if (zbuffer[idx] < P.z) {
				zbuffer[idx] = P.z;
				TGAColor color = model->diffuse(uvP);
				image.set(P.x, P.y, TGAColor(color.r * intensity, color.g * intensity, color.b * intensity, color.a * intensity));
			}
		}
	}
}

三角形光栅化

代码自tinyrenderer, Lesson2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 这个算法本质是通过三角形左右两边y各自比例关系来确定x绘制的起始和终止位置。
void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage& image, TGAColor color) {
	if (t0.y == t1.y && t0.y == t2.y) return; // i dont care about degenerate triangles
	if (t0.y > t1.y) std::swap(t0, t1);
	if (t0.y > t2.y) std::swap(t0, t2);
	if (t1.y > t2.y) std::swap(t1, t2);
	int total_height = t2.y - t0.y; // t0是最低点，t1是次高点，t2是最高点
	for (int i = 0; i < total_height; i++) {   // 从最长边的y轴开始遍历, i从低到高递增
		bool second_half = i > t1.y - t0.y || t1.y == t0.y;  // 判断i是否遍历到次高点
		int segment_height = second_half ? t2.y - t1.y : t1.y - t0.y;  // 计算最高点和次高点长度，或次高点和最低点长度，作为分割长度
		float alpha = (float)i / total_height;  // 计算当前遍历i和总长度的比例，记为alpha
		float beta = (float)(i - (second_half ? t1.y - t0.y : 0)) / segment_height; // be careful: with above conditions no division by zero here // 计算当前遍历i和分割长度，记为beta
		Vec2i A = t0 + (t2 - t0) * alpha;  // 当前alpha比例所在位置
		Vec2i B = second_half ? t1 + (t2 - t1) * beta : t0 + (t1 - t0) * beta; // 计算当前beta所在比例位置
		if (A.x > B.x) std::swap(A, B);  // 让A.x总是小于B.x，用于下面遍历
		for (int j = A.x; j <= B.x; j++) {  // 从左到右遍历x轴，进行上色
			image.set(j, t0.y + i, color); // attention, due to int casts t0.y+i != A.y
		}
	}
}

三角形的重心坐标

给定三角形三个点和P，用三个点表达出P：

其中一种方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// Compute barycentric coordinates (u, v, w) for
// point p with respect to triangle (a, b, c)
void barycentric(Point p, Point a, Point b, Point c, float &u, float &v, float &w)
{
    Vector v0 = b - a, v1 = c - a, v2 = p - a;
    float d00 = Dot(v0, v0);
    float d01 = Dot(v0, v1);
    float d11 = Dot(v1, v1);
    float d20 = Dot(v2, v0);
    float d21 = Dot(v2, v1);
    float denom = d00 * d11 - d01 * d01;
    v = (d11 * d20 - d01 * d21) / denom;
    w = (d00 * d21 - d01 * d20) / denom;
    u = 1.0f - v - w;
}

还有一种方法：

1
2
3
4
5
6
7
8
9
10
11
12
Vec3f barycentric(Vec3f A, Vec3f B, Vec3f C, Vec3f P) {
	Vec3f s[2];
	for (int i = 2; i--; ) {
		s[i][0] = C[i] - A[i];
		s[i][1] = B[i] - A[i];
		s[i][2] = A[i] - P[i];
	}
	Vec3f u = cross(s[0], s[1]);  // 判断有向面积是否为0，若为0则共面
	if (std::abs(u[2]) > 1e-2) // dont forget that u[2] is integer. If it is zero then triangle ABC is degenerate
		return Vec3f(1.f - (u.x + u.y) / u.z, u.y / u.z, u.x / u.z);
	return Vec3f(-1, 1, 1); // in this case generate negative coordinates, it will be thrown away by the rasterizator
}

back-face-culling

目的是减少渲染背面被遮挡的三角形，只渲染能被用户观察到的三角形，这通过判断三角形法向量和光线方向的关系来进行。

在顶点数据中，我们将两个三角形都以逆时针顺序定义（如下图所示，正面的三角形是1、2、3，背面的三角形也是1、2、3（如果我们从正面看这个三角形的话））。然而，如果从观察者 当前视角使用1、2、3的顺序来绘制的话，从观察者的方向来看，背面的三角形将会是以顺时针顺序渲染的。我们只有以特定顺序定义三角形（下图是中为逆时针）才会被渲染：

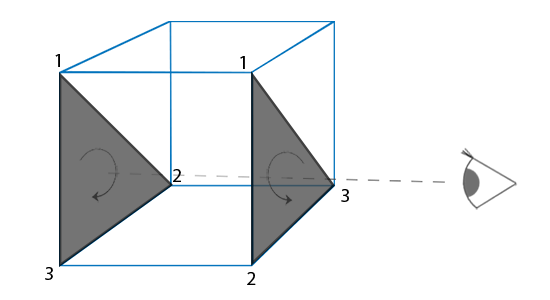
图自Opengl Face culling

根据右手定则可以计算当前顺序定义的三角形的法向量，相机默认位置是-z轴，看向z轴，可以通过比较观察方向是相反，或者和光的反射方向是一致来判断该三角形相对相机是正面还是背面，被渲染或者被剔除，代码自tinyrenderer, Lesson2：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Vec3f light_dir(0,0,-1); // define light_dir

for (int i=0; i<model->nfaces(); i++) { 
    std::vector<int> face = model->face(i); 
    Vec2i screen_coords[3]; 
    Vec3f world_coords[3]; 
    for (int j=0; j<3; j++) { 
        Vec3f v = model->vert(face[j]); 
        screen_coords[j] = Vec2i((v.x+1.)*width/2., (v.y+1.)*height/2.); 
        world_coords[j]  = v; 
    } 
    Vec3f n = (world_coords[2]-world_coords[0])^(world_coords[1]-world_coords[0]); 
    n.normalize(); 
    float intensity = n*light_dir; 
    if (intensity>0) { // 关键代码 
        triangle(screen_coords[0], screen_coords[1], screen_coords[2], image, TGAColor(intensity*255, intensity*255, intensity*255, 255)); 
    } 
}

光线和三角形求交

Moller-Trumbore算法：

图自GAMES101

  • 三角形三维空间的三个顶点。
  • 射线的原点和方向。

输出：

  • 射线和三角形是否有交点。另外 u, v

代码自GAME101 作业五

1
2
3
4
5
6
7
8
9
10
11
12
bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2, const Vector3f& orig,
    const Vector3f& dir, float& tnear, float& u, float& v)
{
    Vector3f E1 = v1 - v0, E2 = v2 - v0, S = orig - v0;
    Vector3f S1 = crossProduct(dir, E2), S2 = crossProduct(S, E1);
    float S1E1 = dotProduct(S1, E1);  // TODO：考虑除数为0的情况。
    if (S1E1 <= 0.0001f) return false;
    tnear = 1.0 / S1E1 * dotProduct(S2, E2);
    u = 1.0 / S1E1 * dotProduct(S1, S);
    v = 1.0 / S1E1 * dotProduct(S2, dir);
    return tnear > 0 && u >= 0 && u <= 1 && v >= 0 && v <= 1 && 1 - u - v >= 0 && 1 - u - v <= 1;
}

Z-buffer(深度测试)

painter’s algorithm不work的场景：

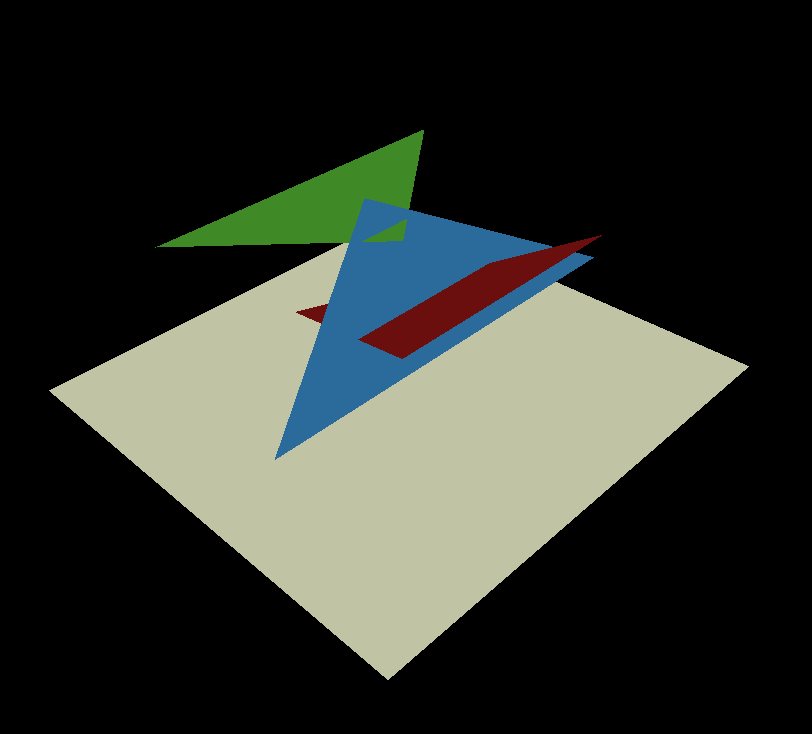
图自tinyrenderer Lesson3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void triangle(Vec3f* pts, float* zbuffer, TGAImage& image, TGAColor color) {
	// 给定三角形三个点，计算最小包围盒
	Vec2f bboxmin(std::numeric_limits<float>::max(), std::numeric_limits<float>::max());
	Vec2f bboxmax(-std::numeric_limits<float>::max(), -std::numeric_limits<float>::max());
	Vec2f clamp(image.get_width() - 1, image.get_height() - 1);
	for (int i = 0; i < 3; i++) {
		for (int j = 0; j < 2; j++) {
			bboxmin[j] = std::max(0.f, std::min(bboxmin[j], pts[i][j]));
			bboxmax[j] = std::min(clamp[j], std::max(bboxmax[j], pts[i][j]));
		}
	}
	// 通过重心坐标计算点是否在三角形内
	// 如果不是则跳过；如果是则判断该点z和深度缓冲该点数值
	Vec3f P;
	for (P.x = bboxmin.x; P.x <= bboxmax.x; P.x++) {
		for (P.y = bboxmin.y; P.y <= bboxmax.y; P.y++) {
			Vec3f bc_screen = barycentric(pts[0], pts[1], pts[2], P);
			if (bc_screen.x < 0 || bc_screen.y < 0 || bc_screen.z < 0) continue;
			P.z = 0;
			for (int i = 0; i < 3; i++) {
				P.z += pts[i][2] * bc_screen[i];
			}
			if (zbuffer[int(P.x + P.y * width)] < P.z) {
				zbuffer[int(P.x + P.y * width)] = P.z;
				image.set(P.x, P.y, color);
			}
		}
	}
}

纹理采样

注意是纹理坐标插值后采样，而不是采样后对纹理进行插值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
Vec3f n = (world_coords[2] - world_coords[0]) ^ (world_coords[1] - world_coords[0]);
n.normalize();
float normal_dot_light = n * light_dir;
void triangle_rgb(Vec3f* pts, Vec3f* normal, Vec2f* texcoords, float* zbuffer, TGAImage& image, TGAImage& texture, float normal_dot_light) {
	Vec2f bboxmin(std::numeric_limits<float>::max(), std::numeric_limits<float>::max());
	Vec2f bboxmax(std::numeric_limits<float>::min(), std::numeric_limits<float>::min());
	Vec2f clamp(image.get_width() - 1, image.get_height() - 1);
	for (int i = 0; i < 3; i++) {
		for (int j = 0; j < 2; j++) {
			bboxmin[j] = std::max(0.f, std::min(bboxmin[j], pts[i][j]));
			bboxmax[j] = std::min(clamp[j], std::max(bboxmax[j], pts[i][j]));
		}
	}
	Vec3f P;
	for (P.x = bboxmin.x; P.x <= bboxmax.x; P.x++) {
		for (P.y = bboxmin.y; P.y <= bboxmax.y; P.y++) {
			// bary centric
			Vec3f bc_screen = barycentric(pts[0], pts[1], pts[2], P);
			if (bc_screen.x < 0 || bc_screen.y < 0 || bc_screen.z < 0) continue;
			P.z = 0;

			// interpolation
			Vec2f uv = { 0, 0 };
			for (int i = 0; i < 3; i++) {
				P.z += pts[i][2] * bc_screen[i];
				uv.x += texcoords[i].x * bc_screen[i] * texture.get_width();
				uv.y += texcoords[i].y * bc_screen[i] * texture.get_height();
			}

			// z-test
			if (zbuffer[int(P.x + P.y * width)] < P.z) {
				zbuffer[int(P.x + P.y * width)] = P.z;
				TGAColor albedo = texture.get(uv.x, uv.y);
				albedo.b = normal_dot_light * albedo.b;
				albedo.r = normal_dot_light * albedo.r;
				albedo.g = normal_dot_light * albedo.g;
				albedo.a = normal_dot_light * albedo.a;
				image.set(P.x, P.y, albedo);
			}
		}
	}
}

SDF

8SSEDT算法

核心：进4退1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
进4
	- - - >
| [?][?][?]
| [?][x][ ]
v [ ][ ][ ]

退1
   < - - -
| [ ][ ][ ]
| [ ][x][?]
v [ ][ ][ ]

进4
   < - - -
^ [ ][ ][ ]
| [ ][x][?]
| [?][?][?]

退1
   - - - >
^ [ ][ ][ ]
| [?][x][ ]
| [ ][ ][ ]
  1. 模板：http://www.codersnotes.com/notes/signed-distance-fields/
  2. case见：https://github.com/Lisapple/8SSEDT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
void compare(std::vector<std::vector<Point>>& grid, Point& p, const int& row, const int& col, int offsetx, int offsety) {
	int row_n = row + offsetx;
	int col_n = col + offsety;
	if (isValid(row_n, col_n)) {
		Point other{ grid[row_n][col_n].dx + offsetx, grid[row_n][col_n].dy + offsety };
		if (other.dist2() < p.dist2()) {
			p = other;
		}
	}
}

void generateSDF(std::vector<std::vector<Point>>& grid) {
	// Pass1
	for (int row = 0; row < HEIGHT; row++) {
		for (int col = 0; col < WIDTH; col++) {
			Point p = grid[row][col];
			compare(grid, p, row, col, -1, -1);
			compare(grid, p, row, col, -1, 0);
			compare(grid, p, row, col, -1, 1);
			compare(grid, p, row, col, 0, -1);
			grid[row][col] = p;
		}

		for (int col = WIDTH - 1; col >= 0; col--) {
			Point p = grid[row][col];
			compare(grid, p, row, col, 0, 1);
			grid[row][col] = p;

		}
	}

	// Pass2
	for (int row = HEIGHT - 1; row >= 0; row--) {
		for (int col = WIDTH - 1; col >= 0; col--) {
			Point p = grid[row][col];
			compare(grid, p, row, col, 0, 1);
			compare(grid, p, row, col, 1, -1);
			compare(grid, p, row, col, 1, 0);
			compare(grid, p, row, col, 1, 1);
			grid[row][col] = p;
		}

		for (int col = 0; col < WIDTH; col++) {
			Point p = grid[row][col];
			compare(grid, p, row, col, 0, -1);
			grid[row][col] = p;
		}
	}
}

Marching Parabolas算法

https://prideout.net/blog/distance_fields/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
void generateSDF(std::vector<std::vector<Point>>& grid) {
	auto isValid = [&](int last, int end) {return last >= 0 && last < end;  };

	// horizontal pass
	for (int row = 0; row < HEIGHT; row++) {
		int last = -1;
		for (int col = 0; col < WIDTH; col++) {
			if (isValid(last, WIDTH) && grid[row][col].dz > grid[row][last].dz + grid[row][last].beta_x) {
				grid[row][col].dz = grid[row][last].dz + grid[row][last].beta_x;
				grid[row][col].beta_x = grid[row][last].beta_x + 2;
			}
			if (grid[row][col].dz != MAX) last = col;
		}

		last = WIDTH;
		for (int col = WIDTH - 1; col >= 0; col--) {
			if (isValid(last, WIDTH) && grid[row][col].dz > grid[row][last].dz + grid[row][last].beta_x) {
				grid[row][col].dz = grid[row][last].dz + grid[row][last].beta_x;
				grid[row][col].beta_x = grid[row][last].beta_x + 2;
			}
			if (grid[row][col].dz != MAX) last = col;
		}
	}

	// vertical pass
	for (int col = 0; col < WIDTH; col++) {
		int last = -1;
		for (int row = 0; row < HEIGHT; row++) {
			if (isValid(last, HEIGHT) && grid[row][col].dz > grid[last][col].dz + grid[last][col].beta_y) {
				grid[row][col].dz = grid[last][col].dz + grid[last][col].beta_y;
				grid[row][col].beta_y = grid[last][col].beta_y + 2;
			}
			if (grid[row][col].dz != MAX) last = row;
		}

		last = HEIGHT;
		for (int row = HEIGHT - 1; row >= 0; row--) {
			if (isValid(last, HEIGHT) && grid[row][col].dz > grid[last][col].dz + grid[last][col].beta_y) {
				grid[row][col].dz = grid[last][col].dz + grid[last][col].beta_y;
				grid[row][col].beta_y = grid[last][col].beta_y + 2;
			}
			if (grid[row][col].dz != MAX) last = row;
		}
	}
}

OBB

基于PCA的生成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
void OBB(std::vector<glm::vec3> points) {
	size_t n = points.size();
	Eigen::MatrixXd data(n, 2);

	// 对数据进行中心化处理
	Eigen::VectorXd mean = data.colwise().mean();
	data.rowwise() -= mean.transpose();

	// 计算数据的协方差矩阵
	Eigen::VectorXd cov = data.transpose() * data / (data.rows() - 1);

	// 对协方差进行特征值分解
	Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eig(cov);

	// 选取前k个最大的特征值对应的特征向量作为主成分
	int k = 2;
	Eigen::MatrixXd pcs = eig.eigenvectors().rightCols(k);

	Eigen::Vector2d maxExtends(INT_MIN, INT_MIN);
	Eigen::Vector2d minExtends(INT_MAX, INT_MAX);
	Eigen::Vector2d eigen_x = pcs.col(0);
	Eigen::Vector2d eigen_y = pcs.col(1);

	if (eigen_x.x() < 0) eigen_x = -eigen_x;
	if (eigen_y.y() < 0) eigen_y = -eigen_y;

	// 求中心点
	Eigen::Vector2d center(0.0, 0.0);
	for (int i = 0; i < n; i++) {
		Eigen::Vector2d tmp(points[i].x, points[i].y);
		center += tmp;
	}
	center = center / n;

	// 求每个点在特征向量上的投影
	for (int i = 0; i < n; i++) {
		Eigen::Vector2d point(points[i].x, points[i].y);
		Eigen::Vector2d displacement = point - center;
		maxExtends.x() = std::max(maxExtends.x(), displacement.dot(eigen_x));
		minExtends.x() = std::max(minExtends.x(), displacement.dot(eigen_x));
		maxExtends.y() = std::max(maxExtends.y(), displacement.dot(eigen_y));
		minExtends.y() = std::max(minExtends.y(), displacement.dot(eigen_y));
	}

	// 矫正中心点，投影空间下
	Eigen::Vector2d HalfLen = (maxExtends - minExtends) / 2.0;
	Eigen::Vector2d offset = HalfLen + minExtends;

	// OBB中点
	center += (eigen_x * offset.x());
	center += (eigen_y * offset.y());

	// OBB四个点
	Eigen::Vector2d lb = center - HalfLen.x() * eigen_x - HalfLen.y() * eigen_y;
	Eigen::Vector2d lt = center - HalfLen.x() * eigen_x + HalfLen.y() * eigen_y;
	Eigen::Vector2d rb = center + HalfLen.x() * eigen_x - HalfLen.y() * eigen_y;
	Eigen::Vector2d rt = center + HalfLen.x() * eigen_x + HalfLen.y() * eigen_y;
}

光线求交算法

https://zhuanlan.zhihu.com/p/138259656

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
bool CalculateIntersectionWithOBB(
	const std::vector<glm::vec3>& bounds,
	const glm::vec3& rayPoint,
	const glm::vec3& rayDir,
	glm::vec3& intersection,
	const glm::vec3& u,
	const glm::vec3& v)
{
	// Calculate the center of the OBB
	glm::vec3 center = (bounds[0] + bounds[1] + bounds[2] + bounds[3]) * 0.25f;

	// Calculate the half-lengths of the OBB along each local axis
	std::vector<float> len{
		glm::length(bounds[2] - bounds[1]) * 0.5f,
		glm::length(bounds[1] - bounds[0]) * 0.5f
	};

	// Define the local axes of the OBB
	std::vector<glm::vec3> axis{ u, v };

	// Initialize the min and max values for the ray's parameter t
	auto ray_t_min = -9999.0f;
	auto ray_t_max = 9999.0f;

	// Test intersection with each axis of the OBB
	for (uint32_t a = 0; a < axis.size(); ++a) {
		auto r = glm::dot(axis[a], rayDir);
		auto s = glm::dot(axis[a], (center - rayPoint));

		if (r == 0.0f) {
			// Ray is parallel to the current axis
			if ((-s - len[a]) > 0.0f || (-s + len[a]) < 0.0f) {
				return false; // No intersection
			}
		}
		else {
			// Ray is not parallel to the current axis
			float r_inv = 1.0f / r;

			auto t0 = (s - len[a]) * r_inv;
			auto t1 = (s + len[a]) * r_inv;

			// Swap t0 and t1 if necessary
			if (t0 > t1) {
				std::swap(t0, t1);
			}

			// Update the ray's min and max parameter values
			if (t0 > ray_t_min) {
				ray_t_min = t0;
			}
			if (t1 < ray_t_max) {
				ray_t_max = t1;
			}

			// Check if the interval is valid
			if (ray_t_max < ray_t_min || ray_t_max < 0.0f) {
				return false; // No intersection
			}
		}
	}

	// Compute the final intersection point
	float t;
	if (ray_t_min > 0.0f) {
		t = ray_t_min;
	}
	else {
		t = ray_t_max;
	}
	intersection = rayPoint + rayDir * t;

	return true; // Intersection found
}