【论文阅读】从Nerf到3D gaussian-splatting的逆渲染

主要记录图形算法、建模思想，不记录公式推导和训练思路：

1. 【Nerf】Representing Scenes as Neural Radiance Fields for View Synthesis.
2. 【Mip-Nerf】Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields.
3. 【Mip-Nerf 360】Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields
4. 【Instant-NGP】Instant Neural Graphics Primitives with a Multiresolution Hash Encoding
5. 【Plenoxels】Plenoxels: Radiance Fields without Neural Networks.
6. 【Ref-NeRF】Ref-NeRF: Structured View-Dependent Appearance for Neural Radiance Fields
7. 【3DGS】3d gaussian splatting for real-time radiance field rendering

概念

渲染（Rendering）是计算机图形学中的一个过程，指的是将计算机生成的三维模型转换成二维图像的过程。这个过程涉及到多个步骤，包括几何变换、光照计算、纹理映射、着色、抗锯齿处理等。渲染的目的是生成视觉上令人满意的图像，它可以用于动画、电影特效、游戏开发、虚拟现实等领域。

逆渲染（Inverse Rendering）是渲染的逆过程，它的目标是从给定的二维图像中恢复出三维场景的信息。这通常涉及到重建场景的几何结构、光照条件、材质属性等。逆渲染在计算机视觉、三维重建、图像编辑等领域有着重要的应用。

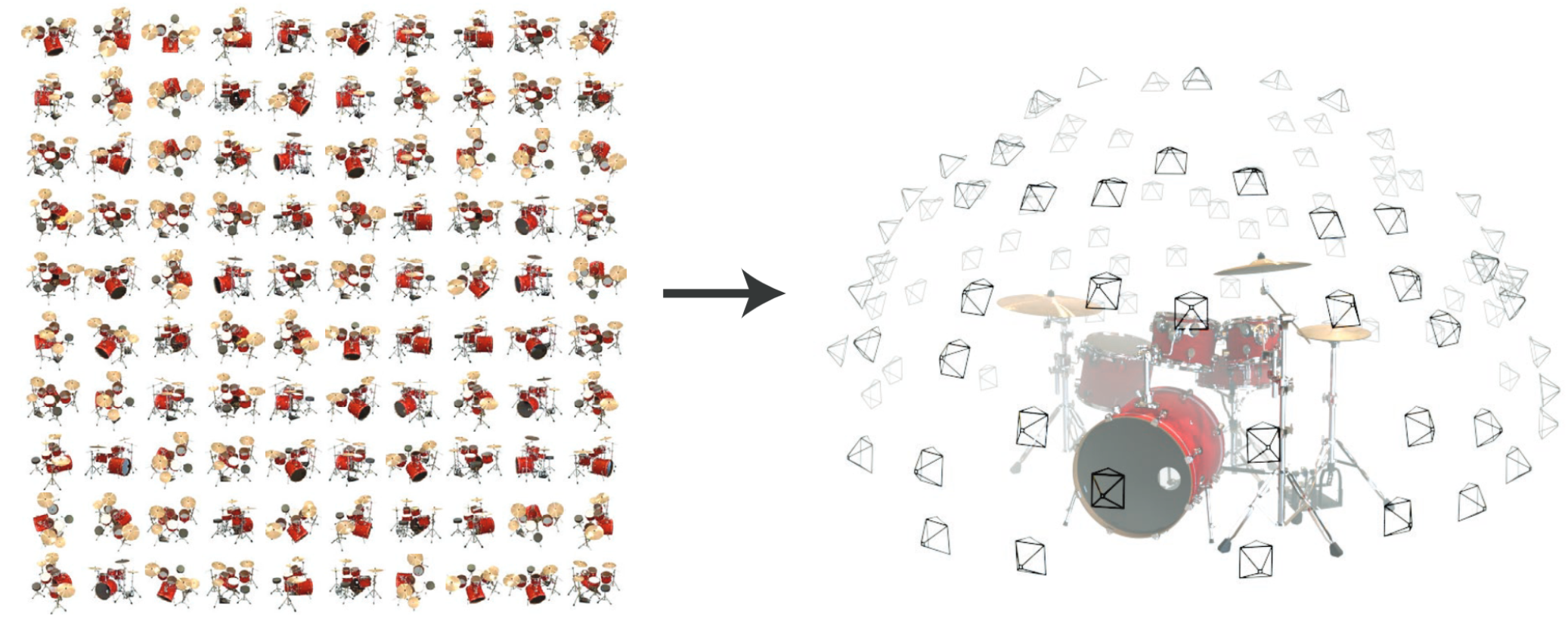
与渲染不同的是，逆渲染的难点在于，不同的三维场景可能产生相似的二维图像，类似于图像复原，这是一个欠定问题，因此需要设计复杂的模型和算法才能求得合理的解。

Nerf和3D Gaussian splatting是近两年比较火的基于深度学习的逆渲染算法。从统计学习数据驱动的角度出发，可以将其认为是训练神经网络从大量不同相机视角渲染得到的图片数据中，学习出该场景的三维表示，因此相关方法有时候会被称为神经渲染（Neural Rendering）；而要让AI工具与图形渲染的相结合，不能忽略的是一个叫可微渲染（Differentiable Rendering）的概念，与传统的渲染管线不同的是，在可微渲染中，渲染过程被设计成可以计算梯度，这使得可以使用基于梯度的优化算法来改进渲染结果或从图像中恢复场景属性。

训练数据

Nerf和3D Gaussian splatting系列方法既可认为是神经渲染，也符合可微渲染的定义。为了更好的理解两者算法，需要认识训练数据的是怎么产生，是怎么构成输入-输出的映射关系的。在笔者认知范围内，常用的数据集类型主要有两种，一种是来自Blender的数据集，还有是一种是来自COLMAP的数据集(当然nerf源码中还有deepvoxels、LINEMOD和llff的数据集，以后补充)。

Blender数据集

Blender是一个开源的3D创作套件，它提供了一整套用于3D建模、渲染、动画、模拟、视频编辑和2D图像编辑的工具。我理解，对于一个在Blender建模的三维场景，可以从较容易地导出其不同视角的图片。以Nerf中常使用的数据集”lego”为例，其主要包含训练、验证和测试集的图片文件夹和json文件，其中json文件中主要记录的时候相机内参 “camera_angle_x” 和各图片对应的相机外参 “transform_matrix”。

所谓的相机内参，描述的是相机自身的属性，与相机的物理特性有关，包括但不限于：

• 焦距（Focal Length）：相机的焦距决定了图像的放大倍数。
• 主点（Principal Point）：通常是图像的中心点，是图像坐标系的原点。
• 像素尺寸（Pixel Size）：每个像素的物理尺寸，影响图像的分辨率。
• 畸变系数（Distortion Coefficients）：描述镜头畸变，如桶形畸变或枕形畸变。

所谓的相机外参，描述的是相机在世界坐标系中的位置和方向，包括：

• 旋转矩阵（Rotation Matrix）：描述相机相对于世界坐标系的方向。
• 平移向量（Translation Vector）：描述相机在世界坐标系中的位置。

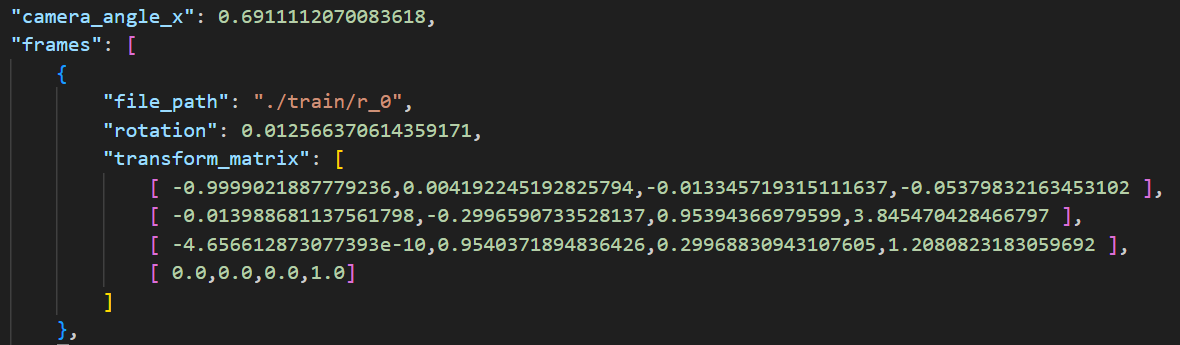
其中”camera_angle_x”是相机的水平视角（FOV, 单位角度），为 $0.69°$，即视野的宽，通过相机的水平视角和图片的宽高可以计算出相机的焦距，Lego数据集中焦距约为 $1111.11mm$。其中焦距f与视角的比例关系如下，即焦距越长，视角越窄（其中的数值因画幅大小而异）：

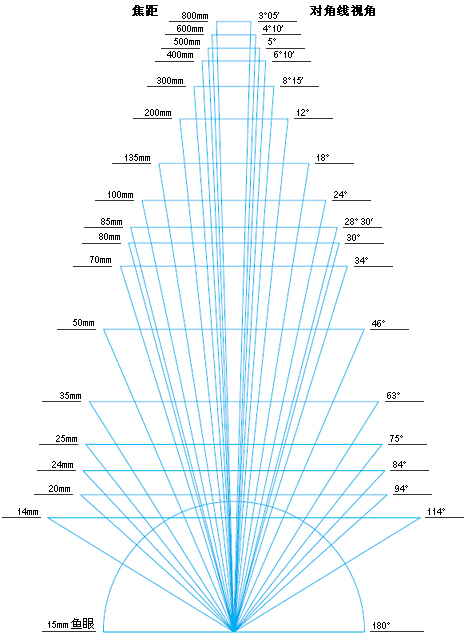
实际中，两者的关系还需考量传感器尺寸大小，以水平大小为例，其一般关系如下：

$$\tan\frac{FOV_x}{2}=\frac{x/2}{f}$$

下图展示的是传感器垂直视角和焦距的关系：

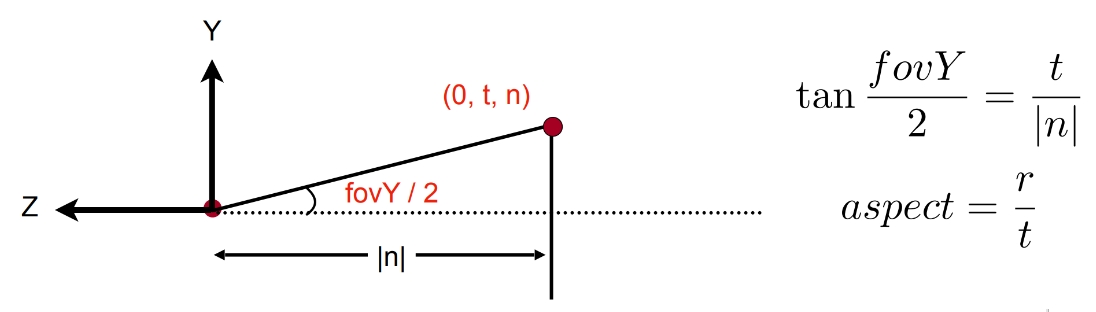
注：”camera_angle_x”一开始我以为是量纲弧度，然而，1弧度约为$1\times \frac{360}{2\pi}\approx57.29577951°$，若为弧度，”camera_angle_x”转换角度大约为$39.59°$，这换算的焦距与实际不符，故起量纲应为角度。

“transform_matrix”是一个视图矩阵（view matrix），在该任务中，每一张图像对应一个transform_matrix，即对应一个相机的位置和旋转角度。

在3D渲染中，为了将三维物体按相机所在位置的二维成像结果正确的表示，其存下如下变换顺序：

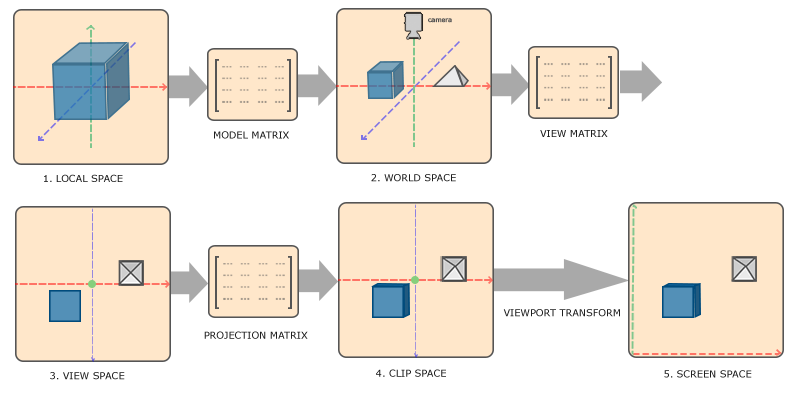
• 模型矩阵（model matrix），用以将模型从其所在局部坐标系转换到世界坐标系中，这似乎是因为物体在建模的时候是以局部坐标系作为参考，而在渲染的过程需要需要统一到世界坐标囍中，model matrix其主要记录了物体的平移、旋转和缩放，这可以通过矩阵的变换来定义。在此任务中，主要是相机绕着物体旋转，而物体保持不动，故model matrix应为单位阵，可认为其不参与变换。

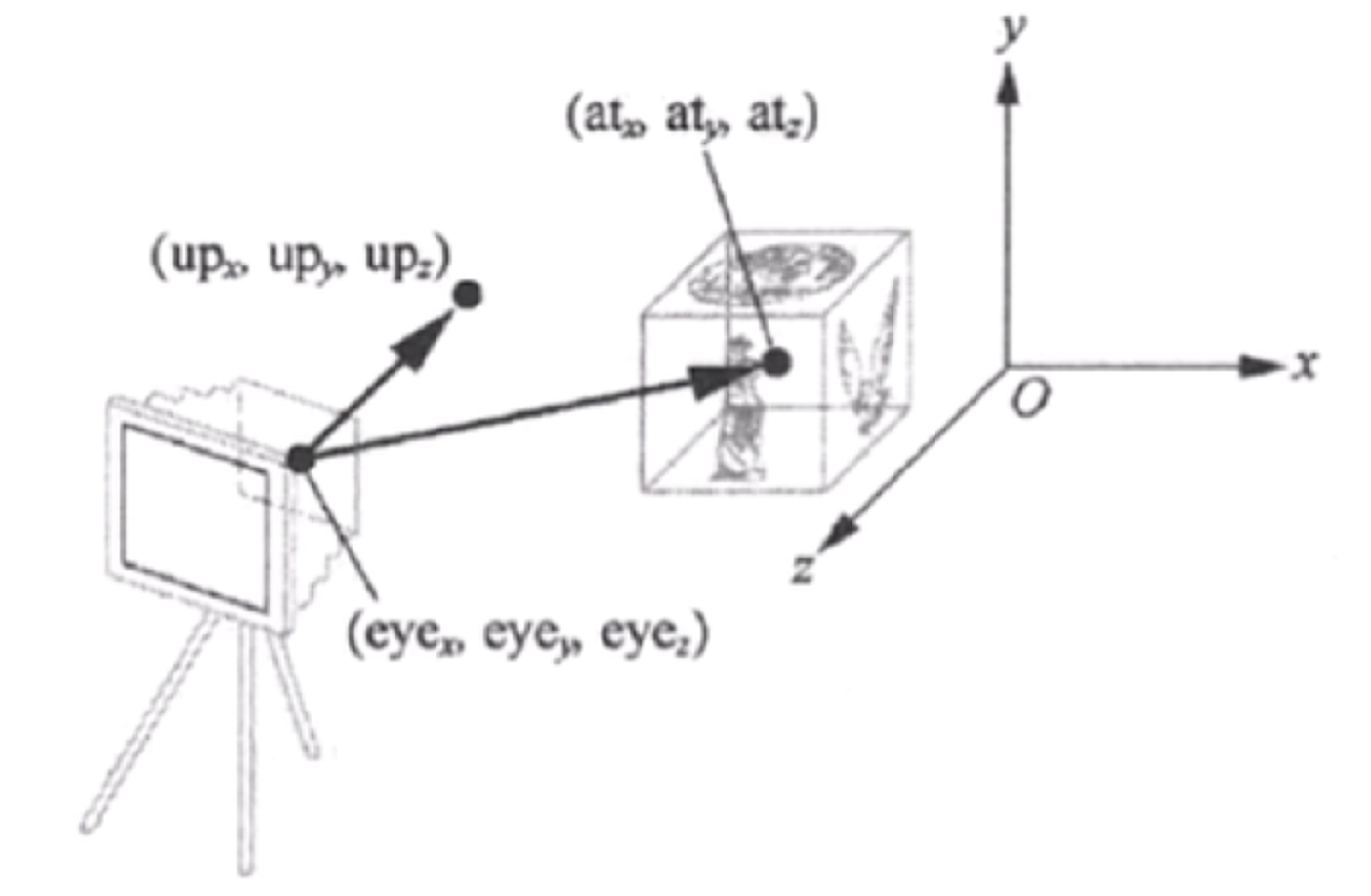
• 视图矩阵（view matrix），用以将世界坐标系中的三维对象转换到相机坐标系中，也就是从观察者（相机）的视角来观察场景。view matrix的含义主要是记录相机的三维空间位置和倾斜旋转（绕xyz轴旋转的角度），这可以直接定义，并在移动/倾斜/旋转镜头的时候调整相关参数。另外，这也可以通过相机位置（camera Position）、相机朝向点（Target Point）和上向量（Up Vector）来定义。后者本质上是通过相机位置和相机朝向点计算相机坐标系下前向量（Front Vector）（图示指向$at$），上向量一般设置为世界坐标系中的$y$轴单位向量，第一次通过对前向量和上向量的叉乘可以求得相机坐标系下的右向量（Right Vector），第二次通过对右向量和前向量的叉乘可以求得相机坐标系下的上向量（图示指向up），通过旋转平移变换以此将世界坐标系转换到坐标系中。

  • 在此任务中，”transform_matrix“定义了该图的对应的view matrix，即相机的三维空间位置和旋转角度。

  

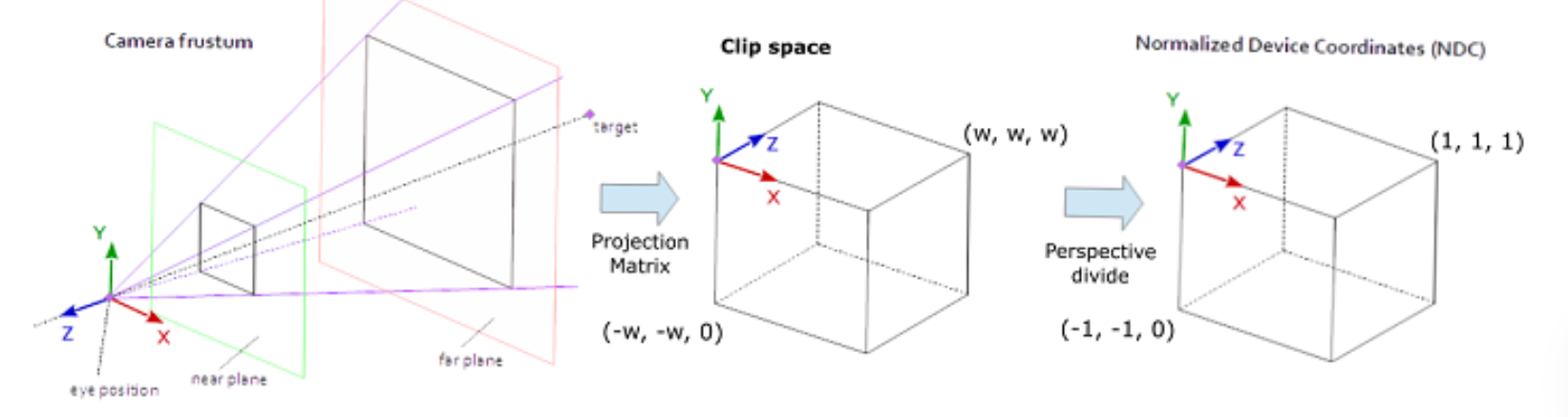
• 投影矩阵（projection matrix)，透视投影是为了获得三维物体在二维屏幕上正确的透视效果，用以将三维空间中的物体映射到二维屏幕空间，即从相机坐标系转换到屏幕坐标系。这可以通过视场（Field of View, FOV, 单位角度）、纵横比（Aspect Ratio）、近裁剪面（Near Plane）和远裁剪面（Far Plane）来定义。

  • 在此任务中，”camera_angle_x“定义了水平视场，图像的宽高定义了纵横比，而代码中定义了远近裁切面（Nerf中分别为2.0和6.0）。
  • 实际上图中还省略了一步，通过投影矩阵的四个参数本质上是定义了一个视椎体（frustum），通过构造出的投影矩阵进行变换能使视椎体的物体被挤压到一个正方体中，也就是裁剪空间（Clip Space），还需通过透视除法（Perspective divide） 将其变换到标准设备坐标（Normalized Device Coordinates，NDC）中，透视除法的作用是将物体的齐次坐标转换常规的三维坐标。在NDC中，xyz各轴取值范围为[-1, 1]，超过此范围的物体，也就是超出视椎体的物体会被裁切而不显示。

• 最后通过视口变换（Viewport Transform），用以将标准设备坐标转换到屏幕空间（Screen Space）中，也就是图像像素空间。

  

Colmap数据集

为了让逆渲染能应用到真实世界图像中，需要一种能从真实世界图像数据集中估计出相机内外参的工具，Colmap是一个流行的开源SfM（Structure from Motion）软件框架，用于从图像集合中进行三维重建，通过运行Colmap，可以得到以下数据：

<location>
|---input
|   |---<image 0>
|   |---<image 1>
|   |---...
|---distorted
    |---database.db
    |---sparse
        |---0
            |---cameras.bin
            |---images.bin
            |---points3D.bin

其中images.bin 记录的是相机外参，主要包括估计出的相机的位移向量tvec和旋转矩阵qvec(由四元数表示)，cameras.bin记录的是相机内参，主要包括视口的宽高，焦距(PINHOLE分为focal_x和focal_y主要是考虑畸变的影响，最后还有图像的中心点，表示是图像坐标系的原点。例子如下所示：

# CAMERA_ID, MODEL, WIDTH, HEIGHT, PARAMS[fx,fy,cx,cy]
# Number of cameras: 1
1 PINHOLE 800 800 1111.1110311937682 1111.1110311937682 400.0 400.0

注：SIMPLE_PINHOLE模式只有一个focal。

区别

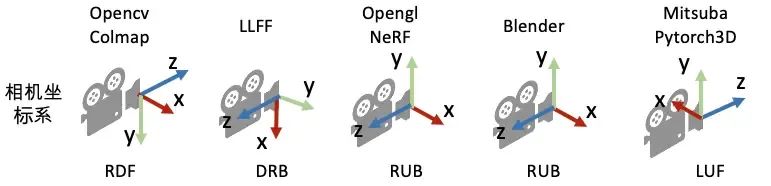
需要注意的是，Colmap上定义的矩阵为行主序，而Blender(NeRF)中的矩阵为列主序；另外，如下图所示，Colmap和Blender数据在y和z轴的方向是相反的，如果要使用相同的训练代码，两者需要转化到同一矩阵形式和坐标空间中。

三维物体的表示方法

三维重建中，三维物体的表示方法有显示表达和隐式表达两种，显式表达是指直接以明确和具体的数学形式定义三维物体或场景的方法。它通常涉及精确的几何数据和结构化的信息。隐式表达是指不直接定义物体的几何形状，而是通过数学函数来隐式地表示物体的存在，物体的内部和外部由这些函数的值来区分。

显式表达包括：

• 点云（Point Cloud）
• 体素（Voxel）
• 三角形网格（Polygon Mesh）
• 深度图（存疑）
• 3D gaussian splatting（三维高斯点云）

隐式表达包括：

• Occupancy function
• Signed Distance Function（SDF）
• Nerf（神经辐射场）

Nerf相关论文

Nerf

NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

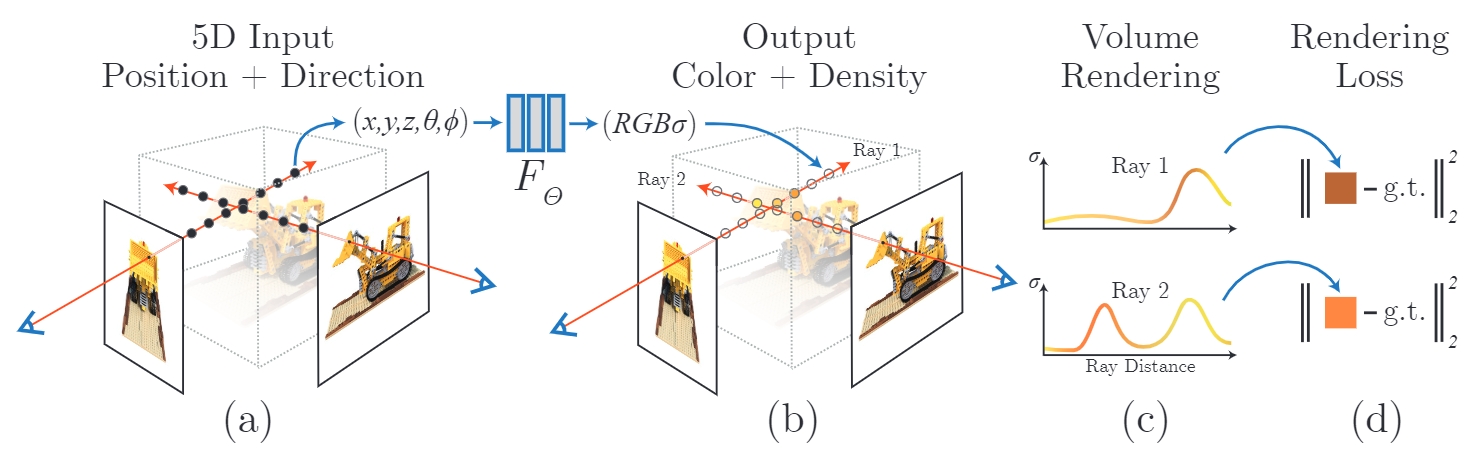
辐射（radiance）在图形学中是一个描述物体表面或光源颜色属性的一个度量，可以看成是颜色和亮度的结合；所谓的神经辐射场目的是使用神经网络隐式地表示一个三维场景；算法的本质是训练一个神经网络以拟合空间各点视角相关的颜色信息，并通过体渲染的方式进行成像，其概要如下：

1. 发射光线：在不同的相机视角下，以(半)焦距为光源，以屏幕上的每个像素为方向，向场景中发射HW条光线，其中H为图像的长，W为图像的宽。射线方程是：

   $$r(t)=o+td$$

   

2. 连续采样：如上图（a）所示，远近平面之间的三维空间将沿着在光线方向进行采样。一般而言，采样空间有两种，一种是在裁剪空间上进行等间隔均匀采样，即采样点线性于深度；另外一种是在视差空间(disparity space)上进行等间隔均匀采样，即采样点线性于深度的倒数，这样做法的动机为了在深度较大的地方使用频率更高的采样率，从而防止锯齿（alias）出现。当然，如果只进行间隔采样，会使网络拟合出一个离散的函数而不是一个“场”，由于不连续，将会使训练出的网络在新视角合成中有很大的质量退化，为了拟合一个连续的函数，算法会在均匀采样点上沿着光线方向加入一些均匀分布的扰动，使得光线上每个点都具有相同的概率被采样到。

   $$t_i\sim \mathcal U[t_n+\frac{i-1}{N}(t_f-t_n), t_n+\frac{i}{N}(t_f-t_n)].$$

   

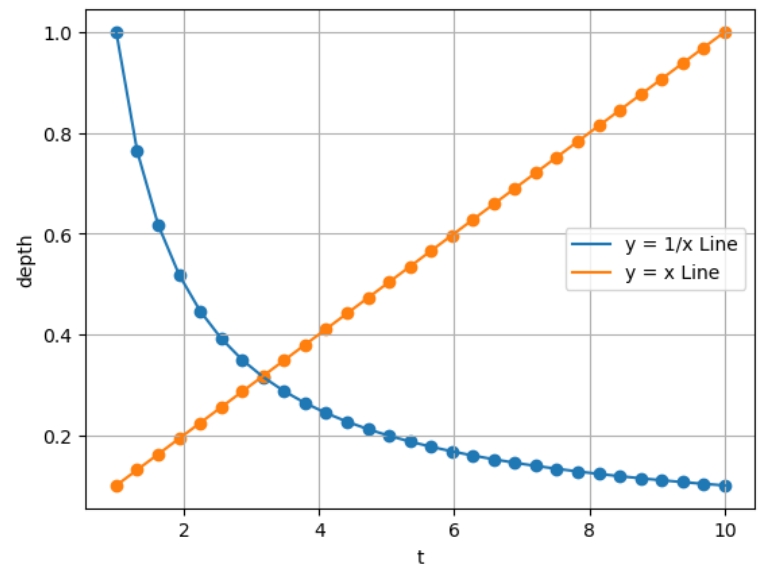
3. 网络输入：通过采样可以得到从近片面出发，沿着射线方向到远平面的一系列采样，这些采样点将按深度由浅到深输入到神经网络中，输入信息包括采样点的三维空间坐标$(x,y,z)$，以及入射方向$(\theta, \phi)$，这是由球面坐标的极角和方位角（Polar and azimuth angles）表示。另外值得一提的是，尽管神经网络是通用函数逼近器，然而相关研究表明：深度网络倾向于学习低频函数，将输入映射到更高维度空间后再传递给网络，能够更好地拟合包含高频变化的数据。为此Nerf中输入的三维空间坐标和球面坐标都将通过位置编码映射到高维特征后再输入到网络中。

   $$\gamma(p)=(\sin(2^0\pi\rho),\cos(2^0\pi\rho),...,\sin(2^{L-1}\pi\rho),\cos(2^{L-1}\pi\rho))$$

4. 体渲染：输入采样点的信息到神经网络中，将被训练输出采样点的颜色和透明度，然而这并不直接作为当前视图成像的输出，而是使用一种叫做体渲染（Volumn Render）的方式逐点累计成像，但体渲染并不是简单地对采样点进行加权平均，而是通过设置一个累计透光率作为权重，该参数会随着累计采样点的个数呈现一种递减的趋势，这是一种模拟光线在不发光粒子中传播中光强损耗的现象，也就是说，深度较浅的采样点会获得更高的权重，随着深度加深，采样点的权重会逐渐衰减；同时，该衰减速度将取决于采样点的透明度，采样点透明度越低，衰减速度越快。如果透光率提前衰减为0，则后续采样点将被抛弃而不参与当前像素的颜色计算；如果在遍历到深度最深的采样点后，透光率仍然大于0，则将使用背景颜色对当前像素的颜色进行累加。

   $$\begin{align*} &\hat C(r)=\sum_{i=1}^N T_i(1-\exp(-\sigma_i\delta_i))c_i, \\ &\text{where}\;T_i=\exp(-\sum_{j=1}^{i-1}\sigma_i\delta_i)\;\text{is accumulated transmittance.} \\ &\sigma_i=t_{i+1}-t_i\;\text{is the distance between adjacent samples.} \\ &c_i\;\text{and}\;\sigma_i\;\text{are the output of network}. \end{align*}$$
   • 在我看来，体渲染在整个算法里是一个非常核心的工具：从渲染角度来看，相较于传统渲染管线光栅化方法的不可微，体渲染是一种可微渲染，这使得神经渲染结果误差能通过梯度进行优化。从优化的角度上，它提供了近采样点比远采样点以更高的权重这样的先验，而不是为每个采样点赋予相同的权重，这符合物理规律，也使得优化更易进行。

5. 分层体积采样（Hierarchical volume sampling）：另外，Nerf会同时优化粗网络（coarse network）和细网络（fine network）做三维空间的分层采样，其中粗网络如上所述在近远平面之间的光线上进行采样，可以认为粗网络在学习整个三维场景的隐式表征，这意味着大量对结果贡献较小的空点也将参与到网络的训练中，并且，在渲染的时候会采样很多空点参与到网络查询中，这将使得渲染低效和不精准。为此，在粗网络输入采样点的基础上，其输出一系列离散点的颜色和透明度估计，此透明度将结合透光率计算出该点的权重，对这些权重归一化后$\hat w_i=w_i/\sum_{j=1}^{N_c}w_j$可以使用逆变换抽样（Inverse Transform Sampling）计算累积分布函数（Cumulative Distribution Function，CDF），从而能根据重要性进行二次采样，二次采样点将输入到细网络进行训练，并输出最终的视角渲染图。

6. 网络训练：网络训练损失是粗细网络采样点体渲染结果与当前视图之前的误差：

   $$\mathcal L=\sum_{r\in \mathcal R}[||\hat C_c(r)-C(r)||^2_2+||\hat C_f(r)-C(r)||^2_2]$$

Mip-Nerf

Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields

Mip-Nerf主要想解决的问题是，虽然原始Nerf在射线上设定了扰动来使采样尽可能连续，但是对于每个像素而言，其只发射的一根射线，这对于神经网络拟合整个三维场景来说采样的密度仍然是不够的，可以认为由于其他分辨率下的一些采样点并没有被训练，这样的网络难以泛化到其他分辨率的新视角合成中，从而产生模糊或者锯齿。解决这个问题的思路容易让人联想到图形学中的多重抗锯齿采样（Multisampling Anti-Aliasing，MSAA）技术，因此，一种可能的方法是一个像素上发射更多的射线进行采样并加权得到最后的渲染结果，然而由于每根射线上的采样点在渲染成像的时候都需要查询网络，这使得这样的算法非常地耗时。

进一步分析，产生模糊的原因是在低分辨率下训练，而在高分辨率上渲染，这是由于网络只学习了低频信息，换言之，其学习到的采样率并不足以渲染一高频图像；产生锯齿的原因则相反，往往是在高分辨率上训练，而在低分辨率上渲染，也就是说，网络学习到的高频信息，在低分辨率图像上会呈现剧烈的像素变化，使得锯齿的产生。因此，另外一个解决思路是联想到图形学中的多级渐远纹理（Mipmap）技术，这也是算法取名Mip-Nerf的启发，其主要思想是在不同分辨率下生成多级纹理贴图，在不同分辨率下使用不同级的纹理贴图渲染图像。对应到神经辐射场中，直接的做法是让一个网络对同一视图下不同分辨率下的渲染结果同时训练，然而，这样的做法也非常耗时，效率低下。

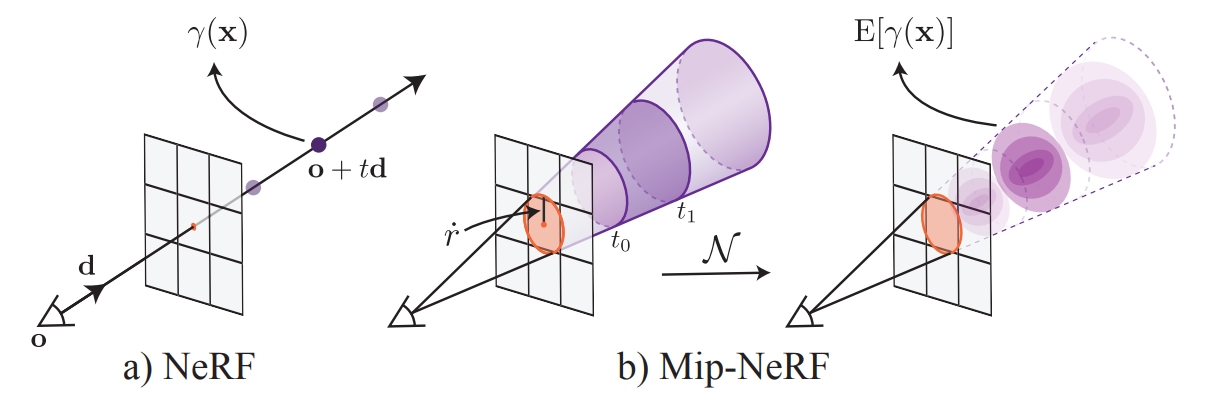
此时，就不得不祭出图形学中的传统艺能——采样，与Nerf在光线上采样不同，Mip-Nerf选择在$[t_{n-1},t_n]$之间的圆锥上进行采样，在Mip-Nerf中的做法是，将该圆锥定义成一个关于$(\mu_t,\sigma_t^2,\sigma_r^2)$的多元高斯分布其中$\mu_t$是平行于光线方向的平均距离，$\sigma_t^2$是平行于光线方向的方差，而$\sigma_r^2$是垂直于光线方向的方差。下面是一个些推理，由于推导比较难，这里只简单梳理一下关系：

$$(\mu_t,\sigma_t^2,\sigma_r^2)$$的这些参数如公式(7)将由中点深度$$t_\mu=(t_0+t_1)/2$$，和半长$$t_\delta=(t_1-t_0)/2$$进行参数化，最后形成的多元高斯分布见公式(8)所示，(8)这个多元高斯分布实际上xyz特征是耦合的，感觉这里的思想是将特征通过正交变换映射到高维特征进行解耦，公式(9)定义了一个分别对不同维度输入做位置编码的矩阵$P$，这里特指的是空间坐标xyz的高维映射矩阵，可以看到其中的线性变换（每$$3\times 3$$矩阵看成是一个线性变换，共$L$次变换到高维特征）是正交的，根据多元高斯分布线性变化的性质，公式(10)展示了可以得到经过位置编码后的高维特征(**IPE feature**)的高斯分布$$(\mu_\gamma,\sum_\gamma)$$，公式(11-12)展示了多元高斯分布分别经过sine和cosine变换后的期望的近似形式，公式(13-14)展示了高斯分布经过高维映射后的特征的期望，这里为了计算协方差矩阵$$\sum_\gamma$$，如(9)所示由于位置编码是分别对不同维度进行高维映射，也就是说两两维度之间并无相关性，也就是说只需要计算各维度变量的边缘分布而无需计算联合分布，也就是说只需计算的对角阵即可得到其协方差矩阵。即便如此，计算高维特征协方差矩阵的对角阵然非常耗时，因此可以通过公式(15-16)计算低维特征协方差矩阵后，再通过位置编码做高维映射得到高维特征协方差矩阵的对角阵。 <img src="./2024-04-21-算法理解之从Nerf到gaussian-splatting/Mip-Nerf相关公式.png" alt="Mip-Nerf相关公式" style="zoom:67%;" /> ## Mip-Nerf 360 **Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields** 这篇论文基于Mip-Nerf改进，Mip-NeRF 360要解决的问题是： 1. 无界场景(unbounded scene)中，这个无界场景是指相机可能指向任何方向，并且内容（前景和背景）可能存在于任何距离，这使得背景范围可能过大，难以设置采样范围，并且由于采样率过低，这将导致结果严重劣化，该问题最早由Nerf++(NeRF++: Analyzing and Improving Neural Radiance Fields.)提出，其解决思路相类似(将背景映射到视差空间)，**解决思路**：而在Mip-Nerf 360中是将Mip-Nerf中使用的高斯分布进行重参数化，如下图所示，定义了一个坐标平滑变化，用于将坐标进行映射：$$

f(x)=
\begin{cases}
\begin{align}
&x\;\;\;\;\;&||x||\le1\
&(2-\frac{1}{||x||})(\frac{x}{||x||})\;\;\;&||x||\gt1
\end{align}
\end{cases}

$$如下图所示，公式的意义是将远景从欧氏距离空间（超出蓝色部分）重参数化到视差空间（橙色部分）。  2. 提升效率。动机是Mip-NeRF用coarse和fine MLP两个网络，其中coarse网络并输出最终结果，其指负责输出一个用于fine MLP的采样权重概率分布（也可以说是密度直方图），这非常耗时。而在Nerf++中，其用两个MLP分别学习该场景的前景和背景。**解决思路**：作者提出训练提议网络（propose network）专门用于预测采样权重概率分布，而无需使用重建损失训练它，因此可以使用一个较浅的网络，该提议网络的输出将用于监督重建网络的训练，这里作者没有使用一个分布损失来约束两者的采样权重概率分布，而是通过约束直方图上界来使两者一致，这背后有一定的理论支撑：$$

\text{bound}(\hat t, \hat w, T)=\sum{j:T\cup{}\hat T_j\ne ∅}{\hat w_j}\
\mathcal L{prop}(t,w,\hat t, \hat w)=\sum_i\frac{1}{w_i}\max(0,w_i-\text{bound}(\hat t, \hat w,T_i))^2

$$ 3. 歧义问题。经过训练的nerf通常表现出"floats"和"background collaps"两个问题，"floats"指的是原本应该表现体积密集空间中，出现了一些小的间断区域，这是由于在训练中该区域只存在于很小一部分数据，由于问题的欠定，只从几个视图网络无法推断出其中的点是否紧密联系，这将导致从别的视角看向该位置会出现一些类似模糊云的现象。"background collaps"指的是远处的表面被错误地建模为靠近相机的密集内容的半透明云的现象，类似的，这也是因为背景或远处的表面在训练集中所含分布权重较低所导致。**解决思路**：加入了一个启发式的正则损失，动机是使得用于重建的采样点密度更集中，这比NeRF在体积密度中注入噪声的方法更有效：$$

L{\text{dist}}(s, w) = \sum{i,j} wi w_j \left( \frac{s_i + s{i+1}}{2} - \frac{sj + s{j+1}}{2} \right) + \frac{1}{3} \sumi w_i^2 (s{i+1} - s_i)

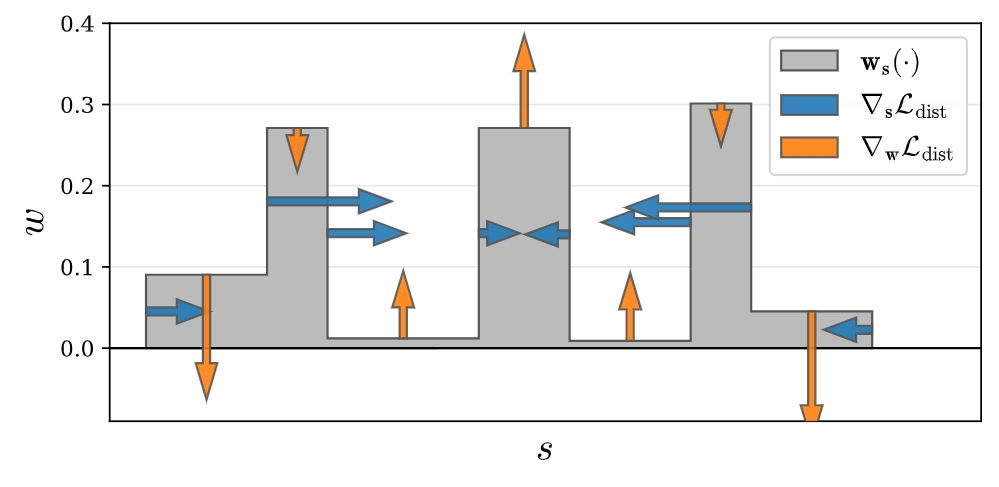
$$
这个正则化器的思想是通过以下方式来鼓励每个光线尽可能紧凑：

1. 最小化每个间隔的宽度：通过正则化器的第一项来实现，该项最小化所有间隔中点对的加权距离。
2. 将远处的间隔拉近：通过正则化器的第二项来实现间隔之间的距离减小来实现。
3. 将权重整合到一个或少数几个附近的间隔中：通过鼓励权重集中在较小的区域内来实现。
4. 在可能的情况下将所有权重推向零：例如，当整个光线都未被占据时。

Instant-NGP

Instant Neural Graphics Primitives with a Multiresolution Hash Encoding

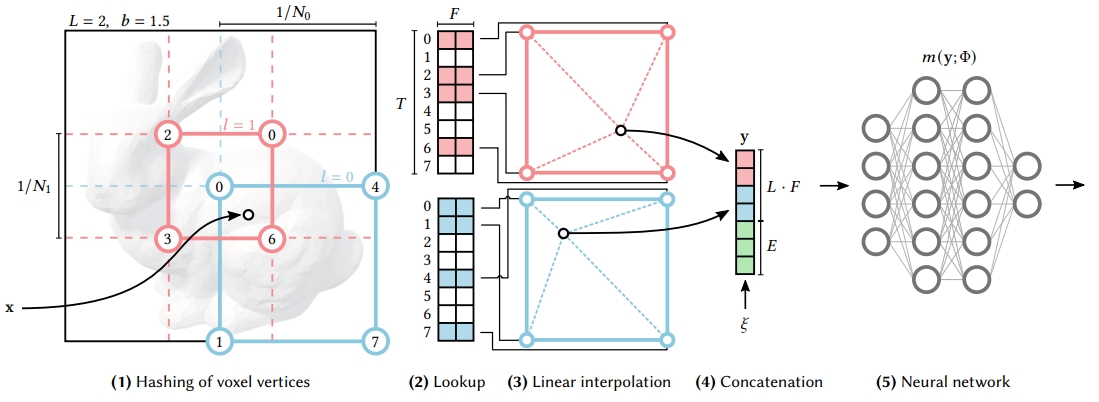
Instant-NGP主要解决的问题是Nerf系列工作训练和渲染耗时较长的问题，其核心主要是使用多分辨率网格结构对场景信息进行记录，但是该多分辨率网格并不是一个结构化数据，而是通过稀疏的多级哈希表来维护。

在每一级哈希表中，哈希函数通过逐维度地对三维坐标进行线性缩放、向下取整、与质数相乘以及模运算，然后将所有维度的结果进行累加，并最终对哈希表的大小进行模运算，得到一个在哈希表大小范围内的索引，这种哈希函数的设计允许神经网络自动学习解决哈希冲突，通过统计学习概率密度较高（物体表面）的三维坐标将被映射在哈希值上，避免了在训练过程中对数据结构进行结构更新的需要。

哈希表的值是该三维坐标在该分辨率下的特征，这是一个可学习参数，在训练中更新。

如下图所示，不同分辨率 $L$ 下的特征 $F$ 和额外输入 $\xi$ 输入到一个浅层MLP中，由于查询哈希表几乎不需要耗时，而相较于原始Nerf中使用的8层MLP网络，这极大地提高了模型训练和体渲染速度，这是一种以存带算的思想。该算法中既有基于体素网格（voxel grid）的结构，也有基于神经网络的结构，可以看成是一种两者混合算法。

Plenoxels

Plenoxels: Radiance Fields without Neural Networks

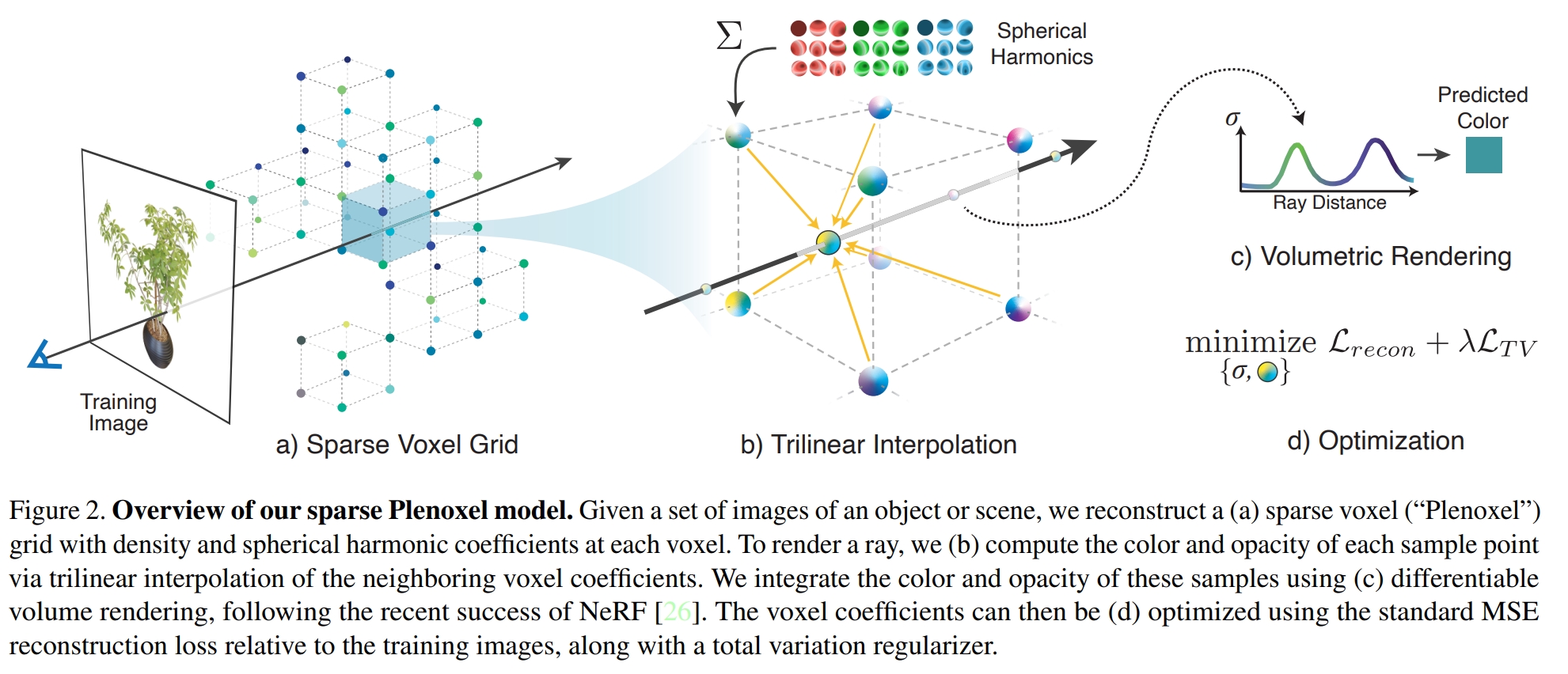
如果把Nerf看成是一个纯网络的算法，Instant-NGP是一个神经网络和体素网格（voxel grid）一类的混合算法，那么Plenoxels就是一个纯体素网格一类的算法。相较于Instant-NGP，其需要解决的问题是如何学习场景中视角（view-dependent）相关的颜色，如下图所示，这里主要通过为网格每个节点学习球谐（spherical harmonics)函数。类似的，场景被表示为一个稀疏的三维体素(grid)网格。在这个网格中，只有非空的体素被存储和处理，这有助于减少计算量和内存使用，这存在了从粗网格到细网格的策略对网格进行压缩裁剪（见PlenOctrees）。为了使结果更加平滑，对相邻网格的各向邻近差值使用Total variation损失进行正则化。

NeILF

NeILF: Neural Incident Light Field for Physically-based Material Estimation

Ref-Nerf

Ref-NeRF: Structured View-Dependent Appearance for Neural Radiance Fields

RawNerf

NeRF in the Dark: High Dynamic Range View Synthesis from Noisy Raw Images

技术要点分类

推理速度

基于神经网络（neural network）和基于体素网格（voxel grid），体素网格能分担一部分场景表达能力，优势是速度更快，代价是存储更大。

逆渲染场景

• forward-facing
• 360°
• real
• unbounded scenes：使用归一化设备坐标(NDC)或多球体图像(MSI)背景模型来扩展其表示，使其能够处理更广阔的视野。

3DGS相关论文

3DGS

3d gaussian splatting for real-time radiance field rendering