记录几种常用的光流方法的原理和思想
参考了
- 光流法-Optical Flow
- 光流估计概念及算法介绍
- 计算机视觉—光流法(optical flow)简介
- Harris角点检测
- Horn-Schunck_method
- Horn-Schunck光流算法
- 啥是TV-L1 OpticalFlow
Motion field
考虑在某个场景下,物体朝着三维空间的某个方向上移动,我们通过相机将物体的运动投影到图像屏幕的平面上形成视频,我们会从视频看到物体的运动方向。当物体在相机前移动时,图像中会有相应的更改。 因此,如果对象上的点 以速度 移动,则可以将成像点 看成以速度 在图像平面上的运动。 所有这些三维空间运动速度投影在二维图像平面的向量的集合形成了运动场(motion field)。
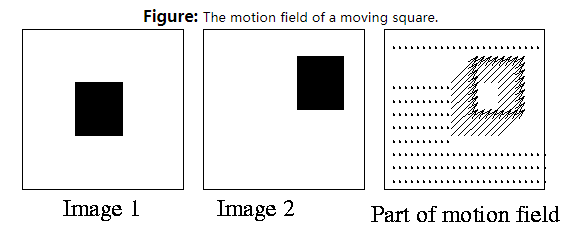
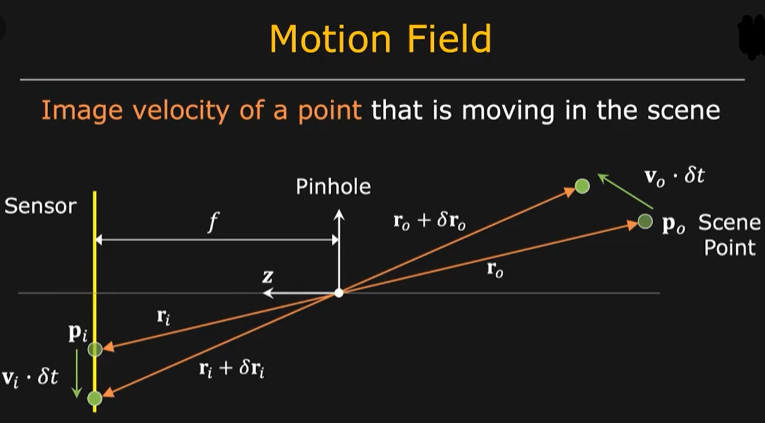
然而我们想通过物体在视频中的移动速度来推导物体在三维空间中的移动速度是不现实的。原因如下,在一个很短的时间段 内,场景中物体的速度为 以及图像的速度 ,我们想要关联这两者的关系。根据位置关系我们能得到以下信息:
其中 表示 在 $z$ 轴上的投影。
图像(运动场)的速度为 (https://www.cse.psu.edu/~rtc12/CSE486/lecture22_6pp.pdf 有一些更详细的):
然而在绝大部分情况下,我们并不能直接通过上式来计算物体的运动场。退而求其次,我们只能通过计算视频光流(optical flow)对物体的运动场进行估计。在理想情况下,光流估计=运动场。然而,也有一些场景光流估计不等于运动场,比如下图中左图是一个单侧光源照射在一个表面质地相同的旋转的球体上,无论球体旋转到什么位置,其反射的光线在相机上成像都是相同的,此时物体的运动场存在,然而没有光流。下图右图中,存在一个围绕静止球体旋转的单侧光源,此时物体并没有旋转,而且其反射的光线在相机上的成像随着光源的旋转而改变,此时物体没有运动场存在,但是却有光流。

又如下图中,旋转灯的运动方向是横向朝右的,而其呈现出来的光流方向却是纵向向下的

同样,在下面两幅图中,图像的纹理并没有移动,而人眼却能观察到光流。


Optical flow
所谓的光流(optical flow)指的是物体或场景相对观测者(相机)运动引起的,往往将在连续帧图像上的特定坐标点上的亮度变化定义为该坐标点的光流矢量,对图像上每个坐标点都计算其光流矢量,则构成图像的光流场,我们希望用光流场来估计物体的运动场,计算光流的算法主要分为稀疏光流算法(sparse optical flow)和密集光流(dense optical flow)两类,常用的光流算法主要有以下几种:
- Lucas-Kanade(LK)光流法 (稀疏光流)
- Horn-Schunck算法
重要假设
基于光流的算法研究往往围绕着以下假设开始建模:
1. 光强恒定假设
2. 瞬时移动假设

考虑 时刻,图像某点在坐标 上的强度(intensity)为 ,在一个很短的时间间隔 后,该点移动到不远处坐标 ,其中 表示一个很小的值,其强度为 ,在该光强恒定假设中,该点在不同时刻的强度恒定不变:
将右式进行一阶泰勒展开可得:
PS:泰勒展开的原式为:
将一阶泰勒展开代入上式可以得到:
令 分别表示光流分别为沿 $x$ 轴与 $y$ 轴的速度矢量,分别表示为图像中像素点的灰度沿 $x, y, t$ 方向的偏导数。在具体操作中,可以很容易的从连续的两帧图像中计算出来。如下图所示,图像中像素点的灰度沿着 $x$ 方向的偏导数 为右边四个方块减去左边四个方块的均值,同理 为上面四个方块减去下面四个方块的均值, 为后面四个方块减去正面四个方块的均值。
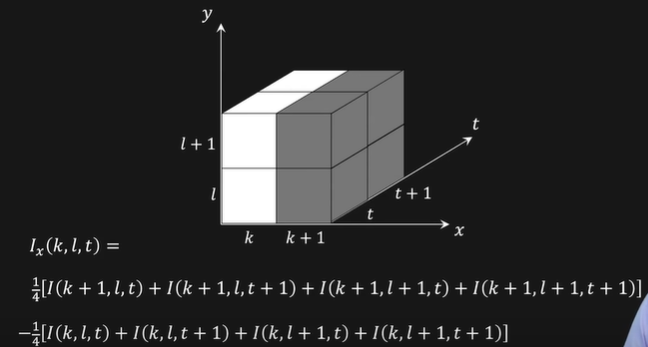
我们现在有了这样的约束方程:
如下图所示,由于 已知,而 未知,对于某点坐标的光流矢量 我们有下图二维坐标的黄线的约束,当然我们可以将该矢量分解为垂直于约束直线方向和平行于约束直线的方向的两个矢量 和 。
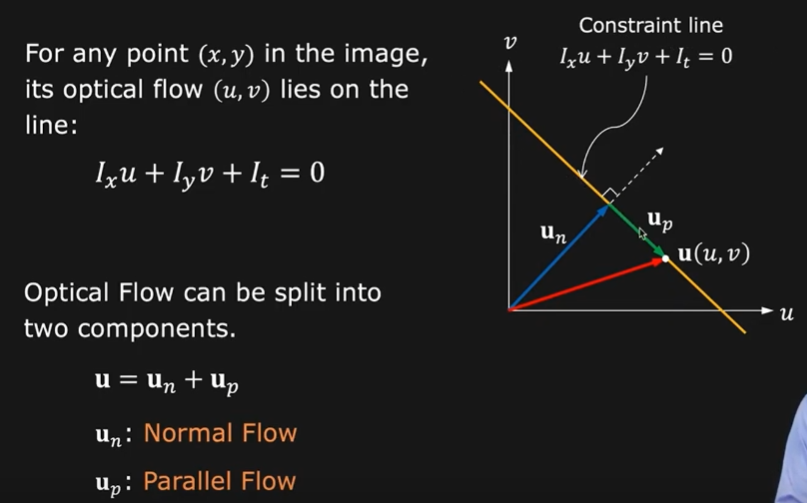
当然我们也可以轻易计算出垂直于约束直线方向的矢量的方向和大小:
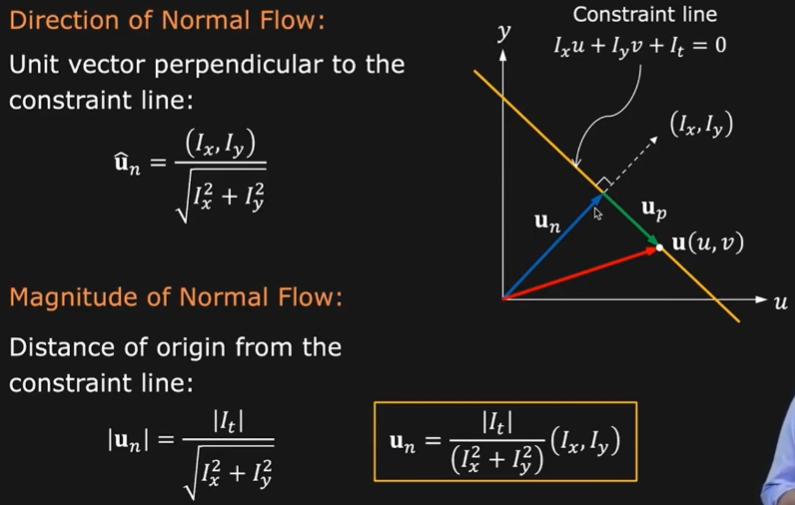
因此问题的难点在于我们无法计算平行于约束直线的光流分量 的大小,当然对于约束直线来说,存在一个方程和两个未知数,因此,仅有该约束,光流问题的求解是欠定的(under constrained),即该存在不同满足单一约束的解。从物理意义上,由于我们观察(假设)的是一个很小的区域的图像像素的灰度变化,如下图孔径问题(aperture problem)所示,在孔径中我们观察到的光流的方向是朝着右下角的方向,然而从整体观察来看,其物体实际运动可能是向下或者是向右的。
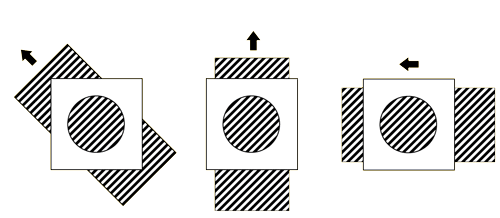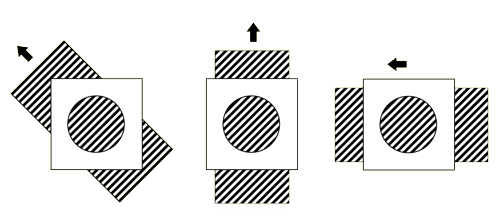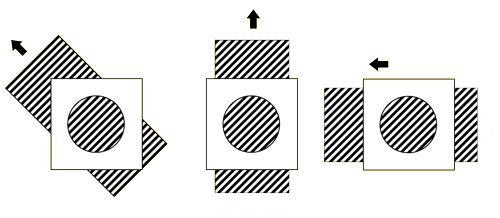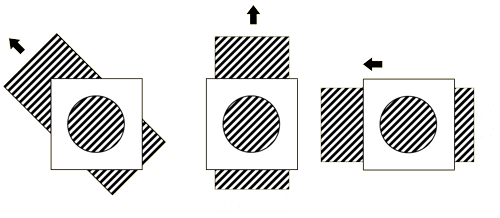
因此我们需要额外的约束来解决光流估计问题,也就是不同光流估计算法提出的出发点和需要解决的问题。
Lucas-Kanade(LK)光流法
LK光流法,进一步假设,图像中一个小的窗口中的每个像素,其运动场也就是光流是相同的。用数学的语言表达,在一个大小为 $n\times n$ 的窗口 $W$ 中的所有像素点 ,其满足:
使用矩阵的形式表达如下:
此时约束方程数()大于未知数(2),该问题会变成一个超定问题,解决该超定问题一种方式看成是解线性最小二乘拟合,使得偏差平方和最小。一种快速和简单的方法如下,将上式两边同时左乘上 $A$ 的转置 得:
可以解得:
其中, 是一个 的矩阵,从拟合效果来说,上式成立存在两个条件:
如果 和 都很小,这说明矩阵的基向量的重要程度很低。如果其中一个特征值 远大于另一个特征值 ,则说明矩阵在一个方向上的基向量很重要,而另一个方向上的基向量重要程度很低。如果这两个条件之一不满足,其求解出来的光流是不准确的。

从实际的物理意义来看,如果窗口定位在光滑区域上,由于光滑区域的各方向的梯度都很小,则其矩阵的 和 都很小,因此估计的光流是不可靠的。

当另一个条件不满足时,其对应的实际物理意义是,窗口定位在边缘的区域上,则垂直于边的梯度很大,平行于边的梯度很小,这样会产生矩阵一个特征值 远大于另一个特征值 的结果,从上面的图可以得知,这样估计得到的光流也是不可靠的。说明了即使是适定问题,其任然有可能是个病态问题,体现在其输入端极小的误差,也可能导致输出值的巨大误差。
那么什么样的区域对于光流的估计是更为准确的呢?结果是窗口定位在富含纹理的区域,这种区域各方向的梯度都比较大而且多样,得到的特征值都比较大,估计的光流较为准确。

当然物理意义上也可以认为是Harris角点检测成立的条件,本质上是用 的特征值 来分类图像中平滑、边缘、角点的区域。
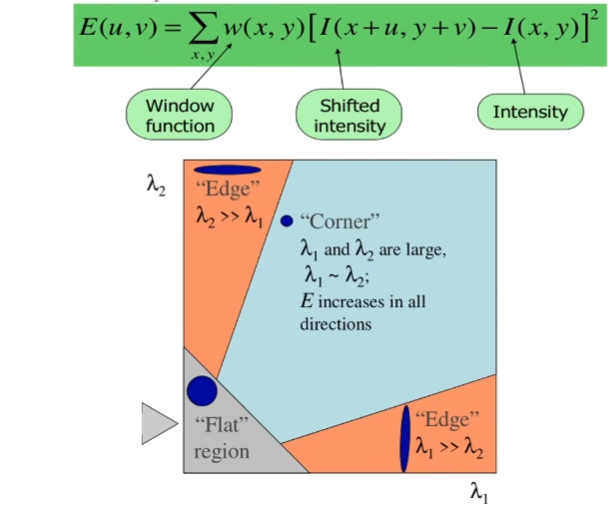
因此LK算法在平滑和边缘的区域表现较差,而在角点或者梯度丰富的区域表现得较好。
Horn-Schunck(HS)光流法
More details: http://www.ipol.im/pub/art/2013/20/
HS光流法是最早提出来估计光流的方法(之一?),他把光强恒定的假设写成需要优化的损失函数,并加上一个平滑约束,新的约束的出发点是运动场在图像上趋于平稳变化,即速度的变化率趋于零,在该假设下,相邻帧的图像中光流分别为沿 $x$ 轴与 $y$ 轴的速度矢量 $u$ 和 $v$ 随着像素点移动而发生的改变是缓慢的,如果变化过大则给于惩罚, 是一个用于权衡重要性的超参数:
目标是为了最小化上述损失函数,其中 是速度矢量 $u$ 对 $x$ 的偏导 ,同理 ,由此看出HS光流法给出的是一个全局约束。
我们可以通过多维欧拉-拉格朗日方程
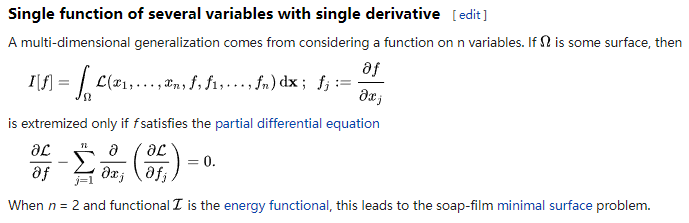
对其进行求解有:
其中 ,代入上式后得:
其中 是拉普拉斯算子,在实际中,拉普拉斯算子是用有限差分进行数值逼近的,常被写为 ,其中 是一个加权平均模板:
用该式替换上式后得:
这是一个二元一次线性方程组,可以对图像中的每个像素求解。然而,由于解依赖于光流场的邻近值,所以一旦邻近值被更新,解就必须迭代更新,利用Cramer规则可以推导出一下迭代公式:
Hierarchical method (金字塔改进)
上述的方法中存在的问题是:
- 鲁棒性较差,无法准确处理原本图象梯度较大的边界区域;
- 并没有解决我们先前提出的针对变化幅度比较大情况下如何准确求解光流的问题。于是乎有了Coarse-to-Fine方法:
针对光流估计的算法还提出了一个改进算法 (Coarse-to-Fine),其要解决的问题是,当物体运动速度很快的时候,即连续两帧物体位置差异较大的情况,那么,在完整的分辨率下,光强恒定和瞬时移动的假设将不成立。这个改进方法的想法是,通过降分辨率的方式来使假设成立,因为在低分辨率情况下,物体运动的位置变化变小了,打个比方,物体在原始分辨率图像下运动4px的像素,在1/4分辨率大小的图像上只运动1px的像素,因此在分辨率降低的情况下可以使得原来的光强恒定和瞬时移动的假设成立。为了计算原始分辨率图像下的光流场,如下图所示,先在低分辨率情况下使用光流算法得到图像的光流场,使用仿射变换将光流场转换到中等分辨率的情况下,利用中等分辨率大小的光流场和前一帧的图像计算得到一个中间插值(interpolation)图像,利用插值帧和后一帧的图像计算中等分辨率下的光流场。以此类推,得到原始分辨率下的光流场 。
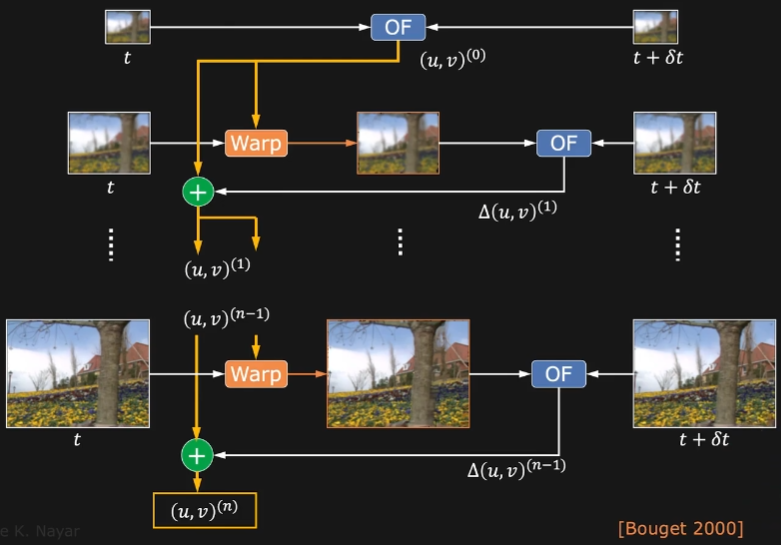
详参考:LK算法改进(金字塔LK)
然而,Coarse-to-Fine方法依然有 其局限性:
① 图象分层方法和插值方法的选择对结果有着极大的影响;
② 由于在Coarse的过程中,原本图象中较为精细结构被忽略了,故而导致对精细结构的估算也就不准确。
Zach光流法(TV-L1 Optical Flow)
More details:http://www.ipol.im/pub/art/2013/26/
HS光流法存在的一个缺点在于其在用二范数惩罚光流矢量的变化率,因此其对于不连续图像序列有很大的惩罚,这使得约束过于强,仅在图像变化方向是连续的时候比较work。因此 TV-L1 光流法为处理连续的图像序列,将约束变成一范数。
Brox光流法
More details:http://www.ipol.im/pub/art/2013/21/article_lr.pdf
加入了梯度恒定的假设即 ,损失函数写成
结果展示


Source code and paper
光流的应用
Optical Mouse
Traffic Monitoring

Video Retiming

Image Stabilization

Face Tracking
Games
